Resources:
- Chapter 3,4,5,6 (Fossen, 2021)
This is the first part of a five-part assignment where you will create a high-fidelity simulation of a ship. The simulation model and its functionality will be built up step-by-step through these assignments
We assume that the geometrical shape of the ship is similar to a rectangular prism
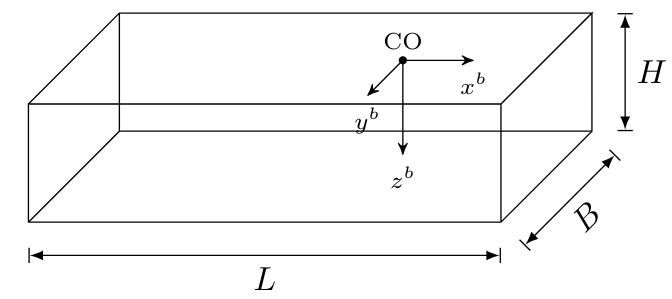 Where m, m, and m.
Where m, m, and m.
Problem 1: Rigid-Body Kinetics of a Rectangular Prism
Resources:
- Chapter 3
- Rigid-Body Kinetics
Goal: Find the rigid-body mass matrix and the Coriolis matrix of the ship (rectangular prism).
a)
The formula for the moment of inertia about the prism’s center of gravity is given by
Which we can write as
We know that since we take the integral of an odd function from to , which becomes zero due to symmetry.
b)
Let . Using the Parallel Axis Theorem we can find the new inertia matrix
And the ratio is
c)
Recall the Skew-Symmetric Matrix
Skew-Symmetric Matrix
The term is the skew-symmetric form of
^36cc79 Where
Link to original
From equation 3.24, 3.29 and 3.30 in the book we can write
Where , is the distance from CG to CO, and are the angular velocities. This gives us
Since we’re only interested in the surge (x), sway (y) and yaw, which are respectively the first, second and last (sixth) state in the rigid-body mass matrix , we get:
We do the same for finding the rigid-body Coriolis and centripetal matrix, :
d)
We can see that is a Skew-Symmetric Matrix. “This is a desired property when designing a nonlinear motion control system since the quadratic form ” (Fossen, page 67), meaning that the Coriolis effect does not change the kinetic energy in the system. A way to think about this is that a change in a state (mode) only redistributes the energy to other states.
e)
When irrotational ocean currents, enter the equations of motion, the Coriolis matrix is unaffected due to it not depending on linear velocity.
Problem 2: Hydrostatics of a Rectangular Prism
Resources:
- Chapter 4
- Hydrostatics
a)
For a floating vessel at rest, Archimedes stated that buoyancy and weight are in balance
Thus giving us the water displacement as
b)
The waterplane area for a prism is constant (as long as it isn’t completely submerged), and is given by:
The hydrostatic force in heave is given by the difference between the gravitational and the buoyancy forces (Eq. 4.12 Fossen)
For small perturbations we can write as (Eq. 4.14 Fossen)
c)
From equation 4.78 in Fossen, we can approximate the heave period as
d)
Computing the metacenter heights for this surface vessel can be done using Eq. 4.34 in Fossen, and is given by
Where , , and is the height from the CB to the CG.
We start by finding and using the Munro-Smith formula, but since the term
Where , we get
We can then find , where is estimated using the Morrish formula:
Combining this, we can get the final expressions for and :
e)
According to definition 4.2 in Fossen, a floating vessel is said to be tranverse metacentrically stable if
And longitudinal metacentrically stable if
For most ships is usually , while is usually . We can therefore conclude that the prism is metacentrically stable.
Problem 3: Added Mass and Coriolis
Resources:
- Chapter 5
- Maneuvering Models
Given the following general matrix of added mass coefficients:
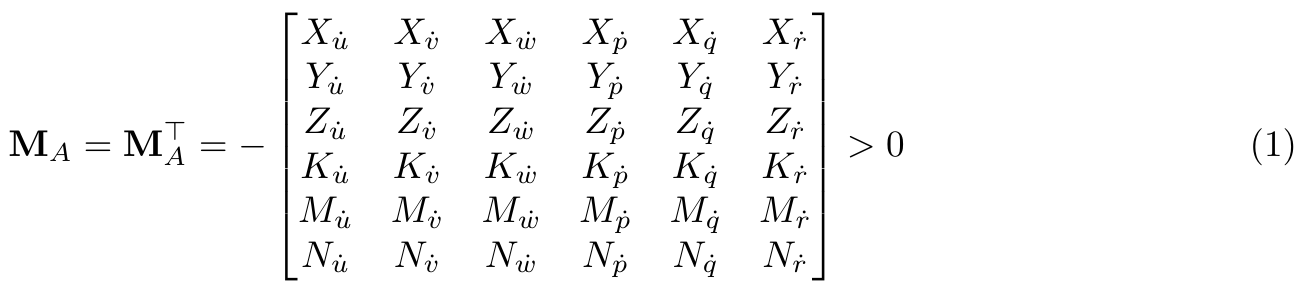
a)
can be rewritten for surge, sway and yaw as
Since (since the inertia for the yaw rate in y rate is equal to the inertia for the y rate in yaw rate), and since we can decouple the surge from steering dynamics due to xz-plane symmetry. Heave, pitch and roll modes are also neglected as we assume small values.
b)
From property 6.2 in Fossen, we know that (Eq. 6.46)
Since we’re only interested in surge,sway and yaw (mode 1,2, and 6) we get:
Where , and (Eq. 6.47 → 6.52).
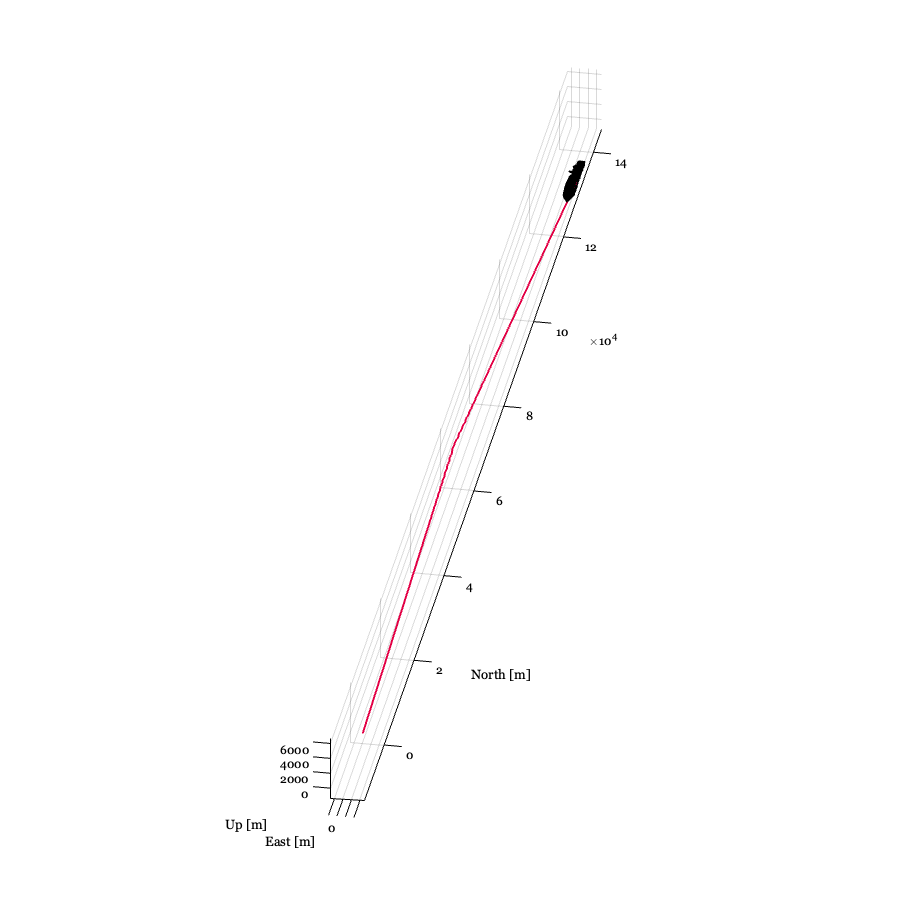
Problem 4: Implementing the Maneuvering Model in Matlab
Goal: Implement the model in Matlab. See the files ship.m and main.m.
a)
This was achieved by adding the added mass matrices, and .
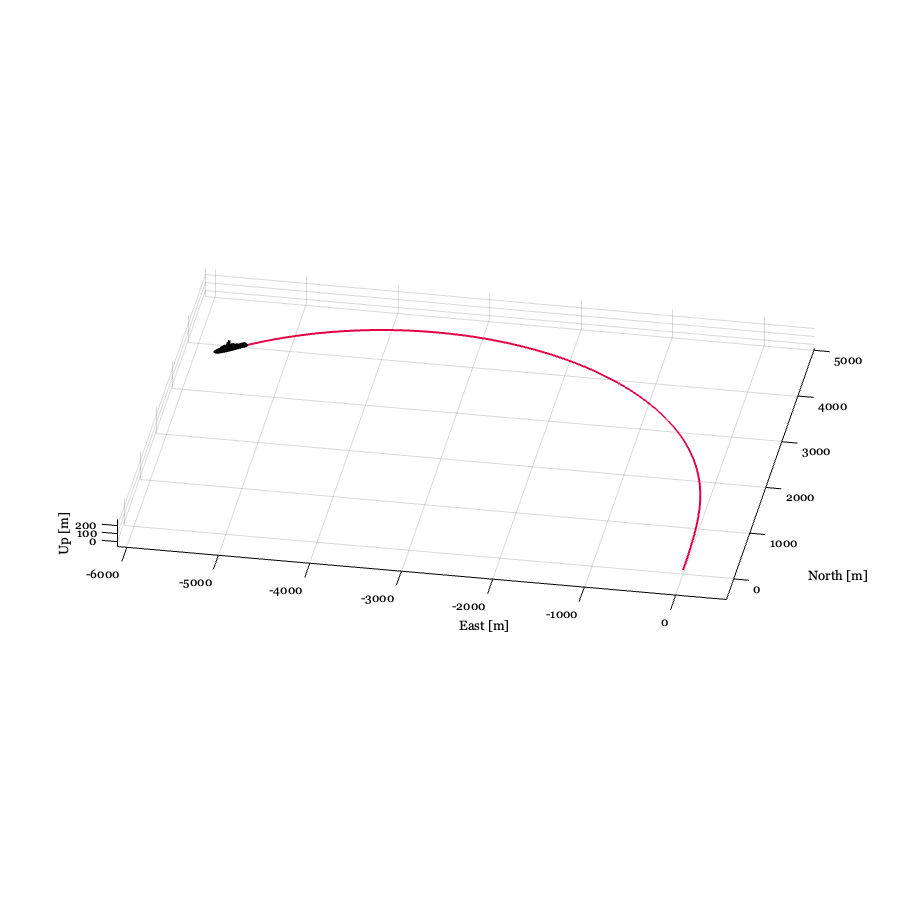
b)
With linear damping for all modes, nonlinear surge damping (Eq. 6.76, 6.77), and cross-flow drag (Eq. 6.87, 6.88).
c)
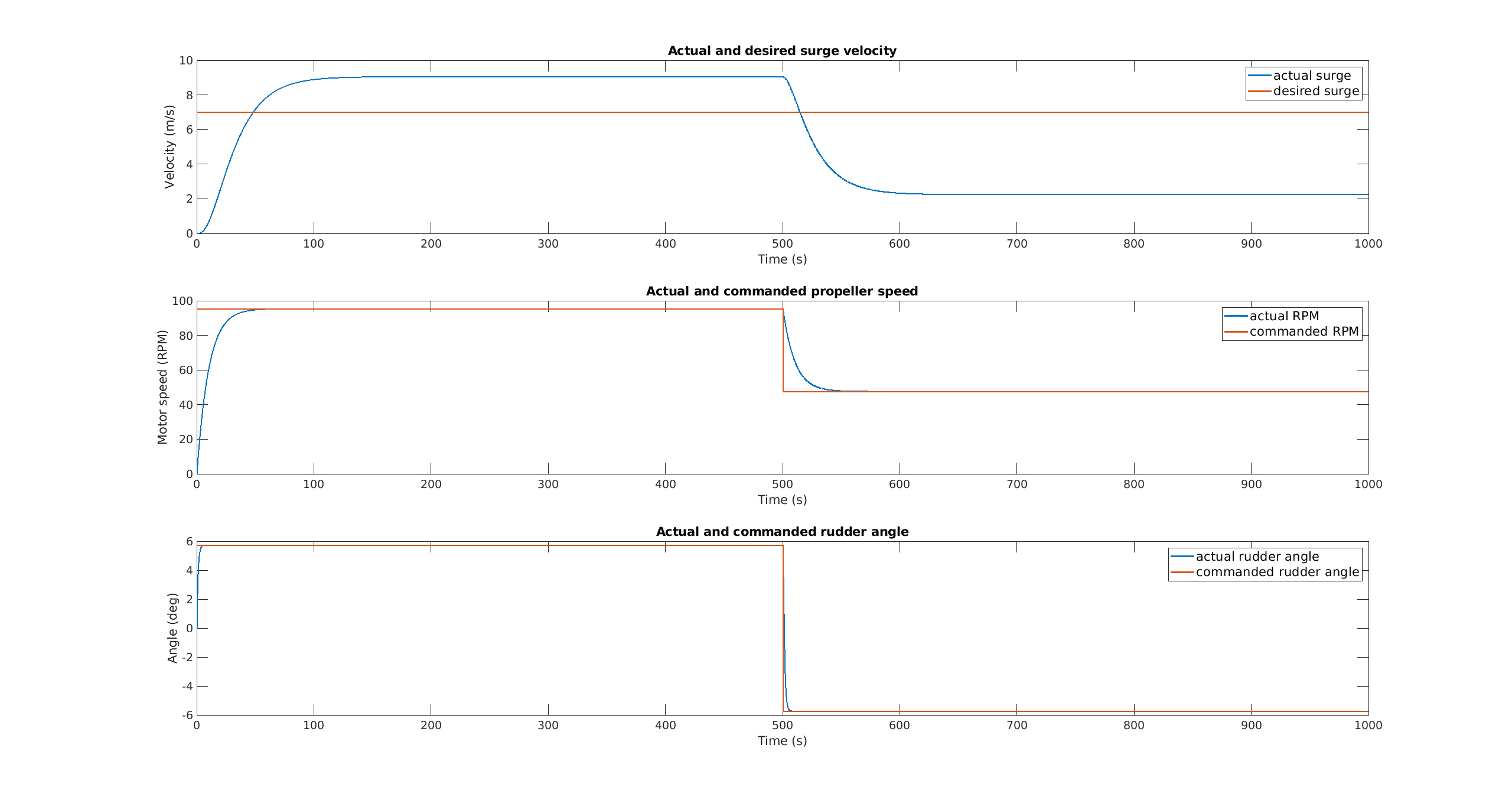
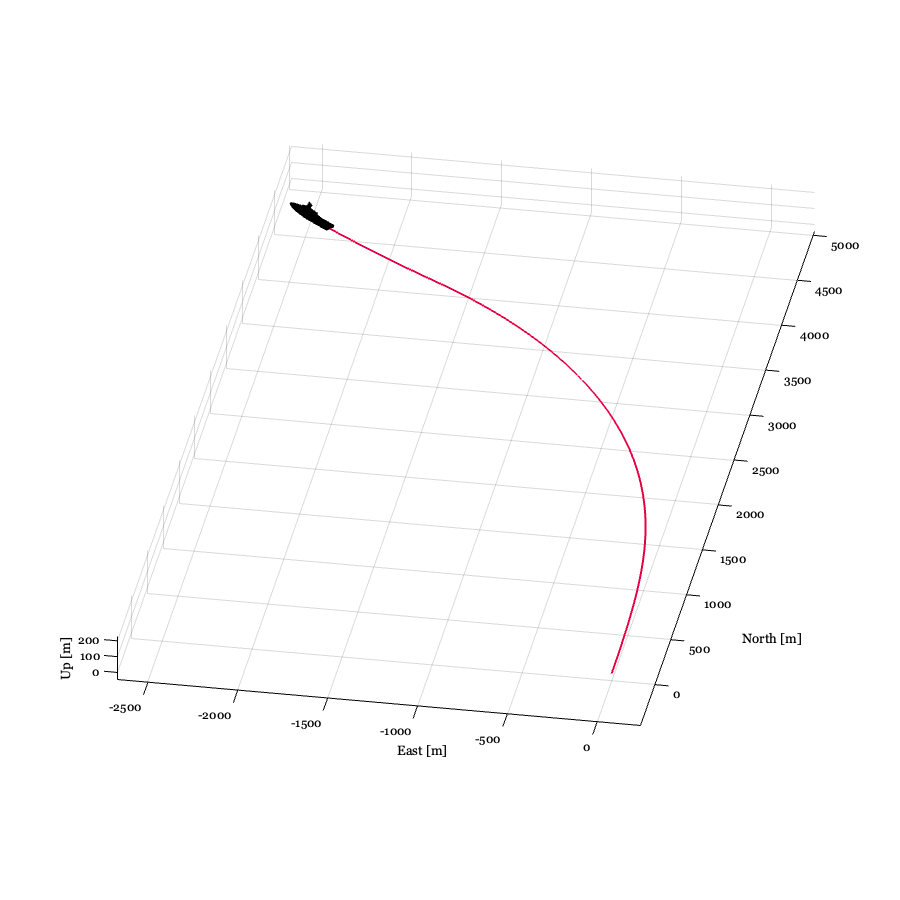
d)
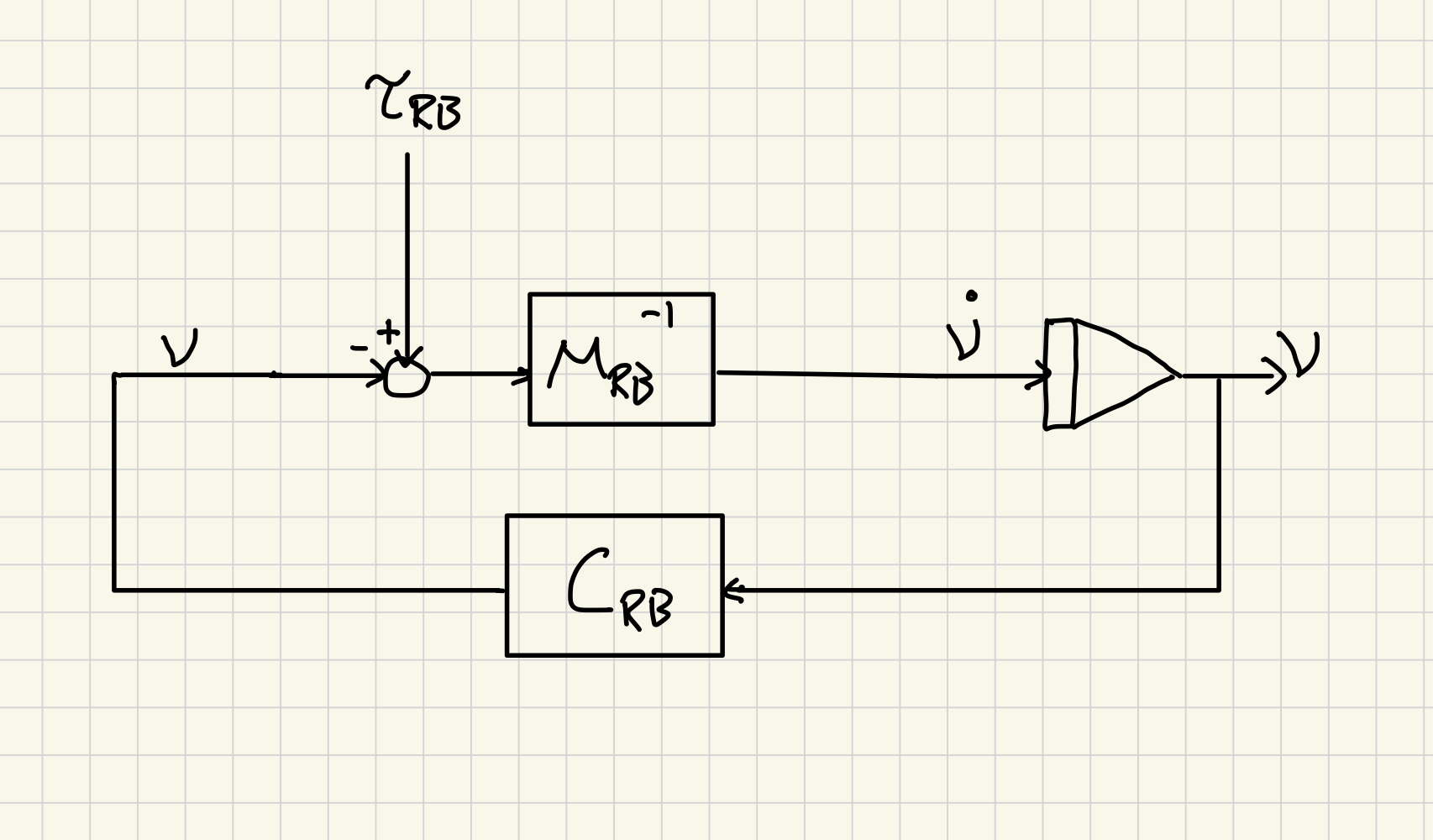
Where
And , as described earlier in the report.