Exercise 8 - Unconstrained Optimization

Problem 1 (25%) Second-Order Necessary Conditions

a)

Theorem 2.3

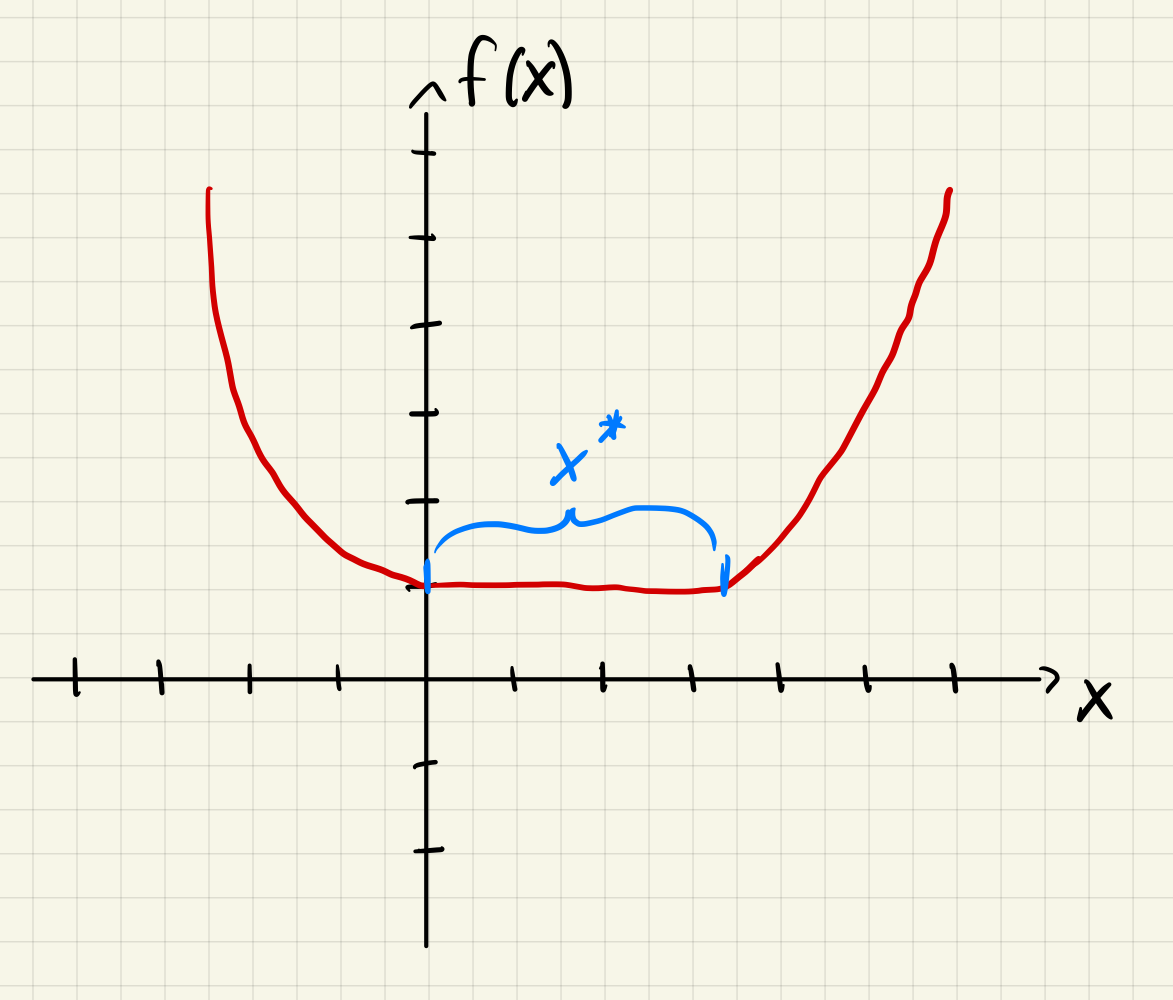
If $x^{\ast }$ is a local minimizer of $f$ and ${\nabla }^{2}f$ exists and is continuous in an open neighborhood of $x^{\ast }$, then $\nabla f(x^{\ast })=0$ and ${\nabla }^{2}f(x^{\ast })$ is positive semidefinite.

Link to original

A visual representation of theorem 2.3

b)

If we think about the scalar case this is similar to what we learned in R2. When the second derivative, $f^{\prime \prime }(x)$, is greater than or equal to zero, $f^{\prime \prime }(x)\ge 0$, we have a minima which is not necessarily strict.

c)

Since the Hessian is not strictly positive (positive semi-definite instead of positive definite), we can not guarantee a strict local minimum.

Problem 2 (40%) The Newton Direction

Consider the model function $m_k$ based on the second-order Taylor approximation

$$m_k(p)=f_k+p^T\nabla f_k+\frac{1}{2}{p}^T{\nabla }^2{f}_{k}p\approx f(x_k+p)$$

a)

We find the Newton direction by finding the direction $p$ that minimizes the function $m_k$

$$\underset{p}{\min }{m}_k(p)$$

We find

$$\frac{\partial }{\partial p}{m}_k(p)=\nabla f_k+\frac{1}{2}({\nabla }^2{f}_k{)}^{T}p+\frac{1}{2}{\nabla }^2{f}_{k}p$$

Since the Hessian of $f_k$ is symmetric we get

$$\frac{\partial }{\partial p}{m}_k(p)=\nabla f_k+{\nabla }^2{f}_{k}p$$

We now need to find the minima (set the equation above equal to zero), giving us

$$p_k^N=-({\nabla }^2{f}_k{)}^{-1}\nabla f_k$$

Q.E.D

b)

The rate of change is given by $\nabla f_k^T{p}_k^N$, which gives us

$$\nabla f_k^T{p}_k^N=-\nabla f_k^T({\nabla }^2{f}_k{)}^{-1}\nabla f_k$$

Meaning that the sign of the rate of change depends on the sign of

$$({\nabla }^2{f}_k{)}^{-1}$$

• If the the Leading Principle Minors are negative, we do not have a descent direction.
• If they are mixed we cannot say if $p_k^N$ is a descent direction.
• If they are $0$ we have a singularity, and it is not invertible, meaning that $p_k^N$ does not exist.

c)

Given the following unconstrained minimization problem with objective function

$$f(x)=\frac{1}{2}{x}^{T}Gx+x^{T}c$$

Where $G=G^T>0$ and $x\in {\mathbb{R}}^n$.

We find the minimizer of $f$

$$\begin{array}{rl}\nabla f& =G{x}^{\ast }+c=0\\ x^{\ast }& =-G^{-1}c\end{array}$$

Where the Hessian is given by

$${\nabla }^{2}f=G$$

Which gives

$$\begin{array}{rl}{p}_k^N& =-({\nabla }^2{f}_k{)}^{-1}\nabla f_k\\ p_k^N& =-G^{-1}(G{x}_k+c)\\ p_k^N& =-x_k-G^{-1}c\end{array}$$

Iterating gives

$$\begin{array}{rl}{x}_{k+1}& =x_k+p_k^N\\ x_{k+1}& =x_k-x_k-G^{-1}c\\ x_{k+1}& =-G^{-1}c=x^{\ast }\end{array}$$

Which means we always reach the optimum in one step

d)

We quickly see that the domain, $x_1^2+x_2^2\le 1$ is convex.

We need the following to be satisfied for the function to be convex

Link to original

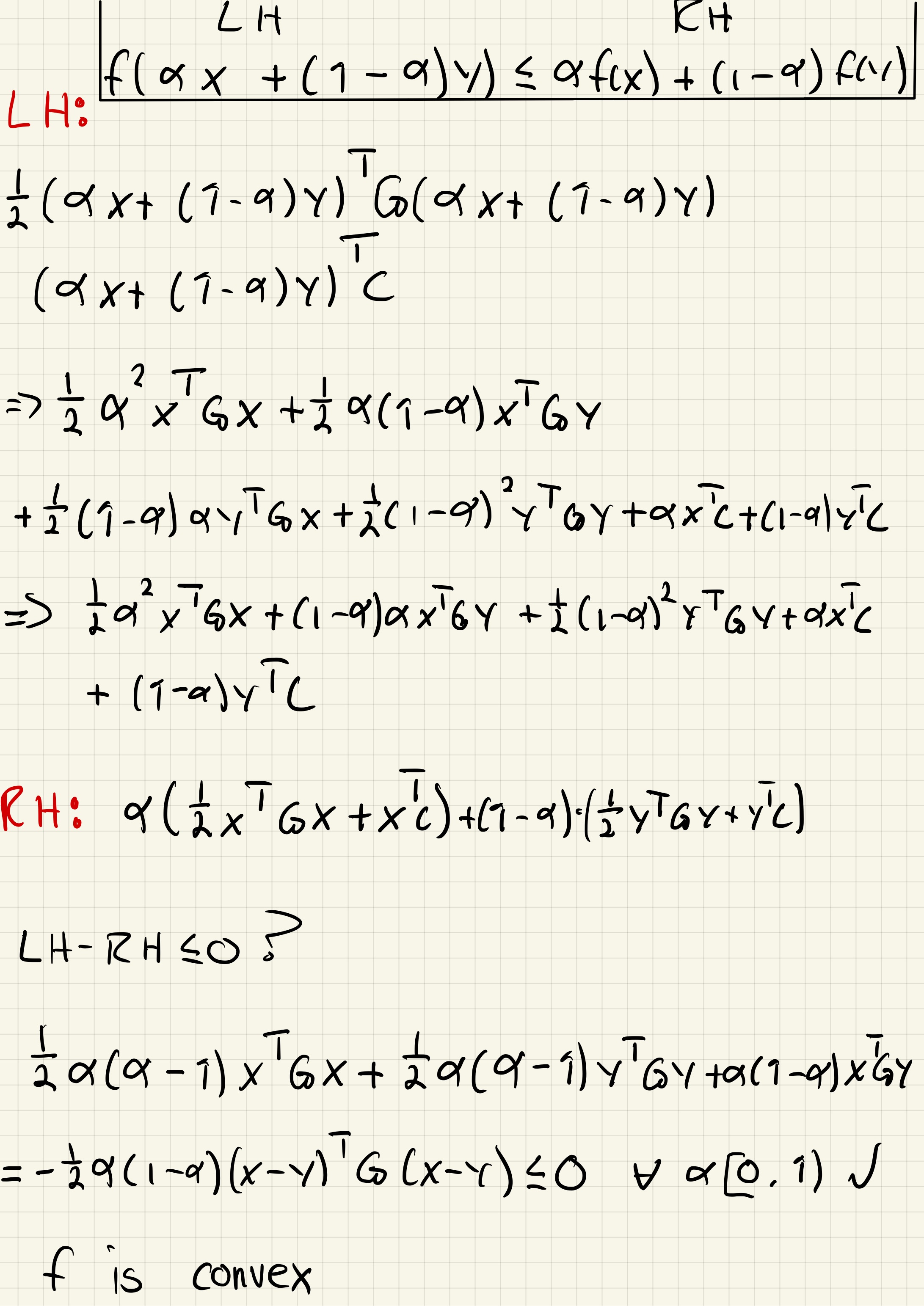
We see that $f$ is convex for all values of $\alpha$ due to $G$ having only positive Leading Principle Minors.

Problem 3 (35%) The Rosenbrock Function

This problem can be found here:

• page=50

Problem

Compute the Gradient $\nabla f(x)$ and Hessian ${\nabla }^{2}f(x)$ of the Rosenbrock Function

Link to original

Show that $x^{\ast }=[1,1{]}^T$ is the only minimizer of this function, and that the Hessian matrix at that point is a Positive-Definite Matrix.

---

The Gradient is given by

$$\nabla f(x)=\left[\begin{array}{c}\frac{\partial f}{\partial x_1}\\ \frac{\partial f}{\partial x_2}\end{array}\right]=\left[\begin{array}{c}-400(x_1{x}_2-x_1^3)+2x_1-2\\ 200(x_2-x_1^2)\end{array}\right]$$

---

And the Hessian is given by

$$\begin{array}{rl}{\nabla }^{2}f(x)& =\left[\begin{array}{cc}\frac{\partial }{\partial x_1}(-400(x_1{x}_2-x_3^2)+2x_1-2)& \frac{\partial }{\partial x_2}(-400(x_1{x}_2-x_3^2)+2x_1-2)\\ \frac{\partial }{\partial x_2}200(x_2-x_1^2)& \frac{\partial }{\partial x_2}200(x_2-x_1^2)\end{array}\right]\\ {\nabla }^{2}f(x)& =\left[\begin{array}{cc}-400x_2+1200x_1^2+2& -400x_1\\ -400x_1& 200\end{array}\right]\end{array}$$

---

We then solve $\nabla f(x^{\ast })=0$ to find the minimizer $x^{\ast }$

$$\begin{array}{rl}\nabla f(x^{\ast })& =0\\ \left[\begin{array}{c}\frac{\partial f}{\partial x_1}\\ \frac{\partial f}{\partial x_2}\end{array}\right]=\left[\begin{array}{c}-400(x_1{x}_2-x_1^3)+2x_1-2\\ 200(x_2-x_1^2)\end{array}\right]& =0\end{array}$$

The second equation gives us

$$x_2=x_1^2$$

Putting this into equation one gives

$$x_1=1,x_2=1$$

Meaning that $x^{\ast }=\left[\begin{array}{c}1\\ 1\end{array}\right]$ is the only minimizer of the Rosenbrock Function.

---

The Hessian at this point is given by

$${\nabla }^{2}f(x^{\ast })=\left[\begin{array}{cc}802& -400\\ -400& 200\end{array}\right]$$

We check the Leading Principle Minors

$$\begin{array}{rl}\text{1. Order Leading Principle Minor}& :\\ \boxed{802}& \\ \text{2. Order Leading Principle Minor}& :\\ 802\cdot 200-(-400{)}^2=\boxed{400}& \end{array}$$

Since both are strictly positive, the Hessian is positive definite at $x^{\ast }$.