P=NP

Dersom man kan sjekke et problem kjapt (Altså et NP problem), betyr det at man også kan finne en løsning kjapt (Altså et P problem)? Med andre ord, er de problemene vi kan verifisere Polynomisk tid også løselige i Polynomisk tid?

---

Fra det vi fant ut i Kompleksitetsklassene vet vi at

$$\begin{array}{r}P\subseteq NP,\text{ce}ogNPC\subseteq NP\end{array}$$

Ethvert problem i NP (og naturligvis også P), kan reduseres til etthvert problem i NPC. Krav for å bevise P=NP:

• Hvis vi kan vise at ett NP-komplett problem (NPC) har en løsning i Polynomisk tid, altså at det er i P, kan vi vise at P=NP.

---

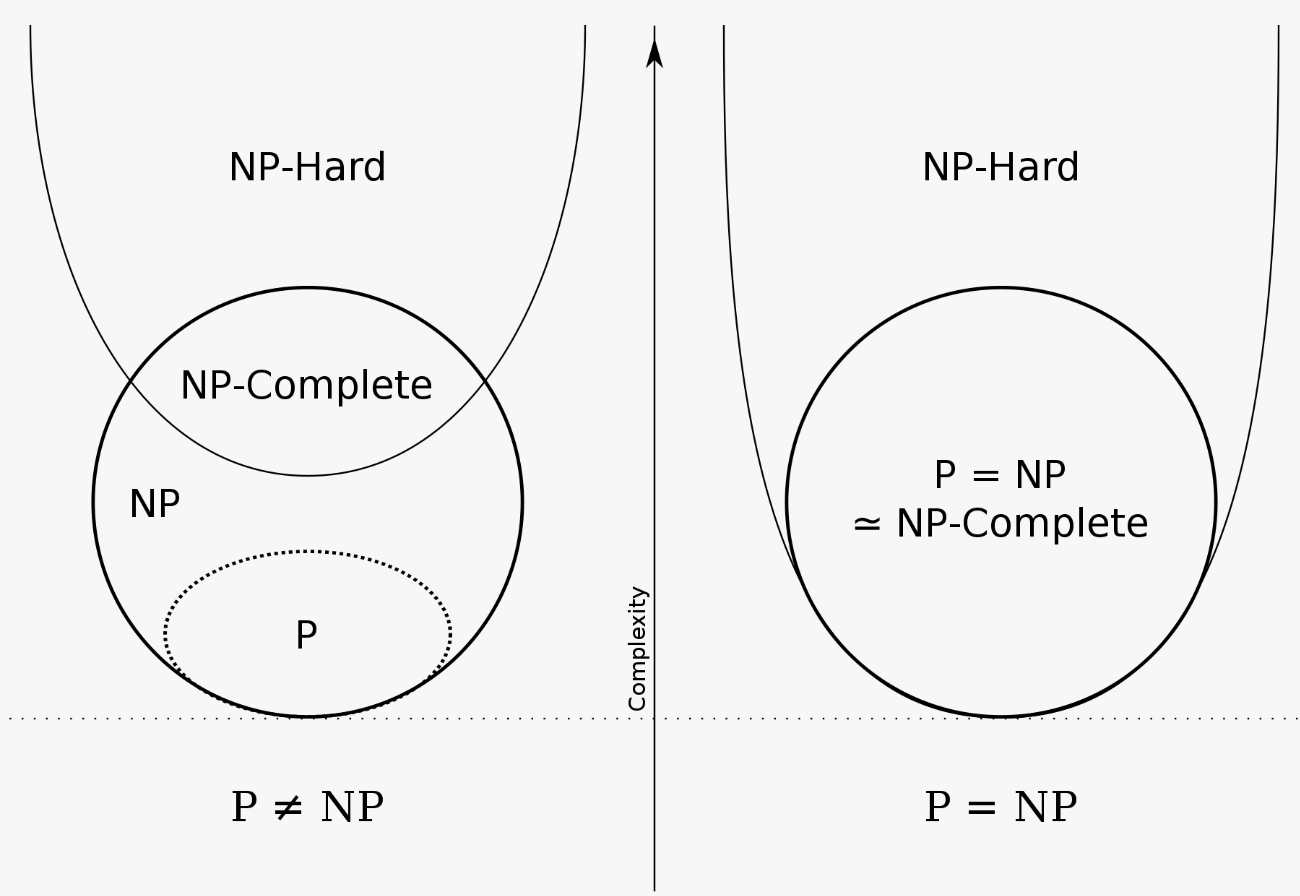
De to antatte mulighetene, enten $P\ne NP$, eller $P=NP$.