Assignment 2 - Kinematics 1

Kinematics Lecture Notes.pdf

---

Problem 1 (Rotation transformation in 2D)

Given the following reference frames (NED-frame and s-frame)

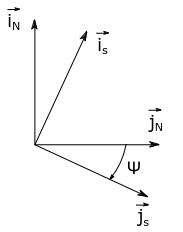
a) Since we have a rotation with the angle $\psi$, we can write the new frame as a result of the transformation

$$\begin{array}{rl}{\vec{i}}_s& ={\vec{i}}_N\cos (\psi )+{\vec{j}}_N\sin (\psi )\\ {\vec{j}}_s& ={\vec{j}}_N\cos (\psi )-{\vec{i}}_N\sin (\psi )\end{array}$$

b) Given $\vec{v}={\zeta }_1{\vec{i}}_s+{\zeta }_2{\vec{j}}_s$, we can express this as through the unit vectors of the NED-frame given the expression we found in a)

$$\begin{array}{rl}\vec{v}& ={\zeta }_1({\vec{i}}_N\cos \psi +{\vec{j}}_N\sin \psi )+{\zeta }_2({\vec{j}}_N\cos \psi -{\vec{i}}_N\sin \psi )\\ \downarrow & \\ \vec{v}& =({\zeta }_1\cos \psi -{\zeta }_2\sin \psi ){\vec{i}}_N+({\zeta }_1\sin \psi +{\zeta }_2\cos \psi ){\vec{j}}_N\end{array}$$

Where ${\chi }_1={\zeta }_1\cos \psi -{\zeta }_2\sin \psi$ and ${\chi }_2={\zeta }_1\sin \psi +{\zeta }_2\cos \psi$

c) We find the rotation matrix, $R_s^N(\psi )$.

$$R_s^N(\psi )=\left[\begin{array}{cc}\cos \psi & -\sin \psi \\ \sin \psi & \cos \psi \end{array}\right]$$

Such that $v^N=\left[\begin{array}{c}{\chi }_1\\ {\chi }_2\end{array}\right]=R_s^N(\psi )\left[\begin{array}{c}{\zeta }_1\\ {\zeta }_2\end{array}\right]=R_s^N(\psi )v^s$.

Problem 2 (Barge with a crane)

Given the figure with the following reference frames 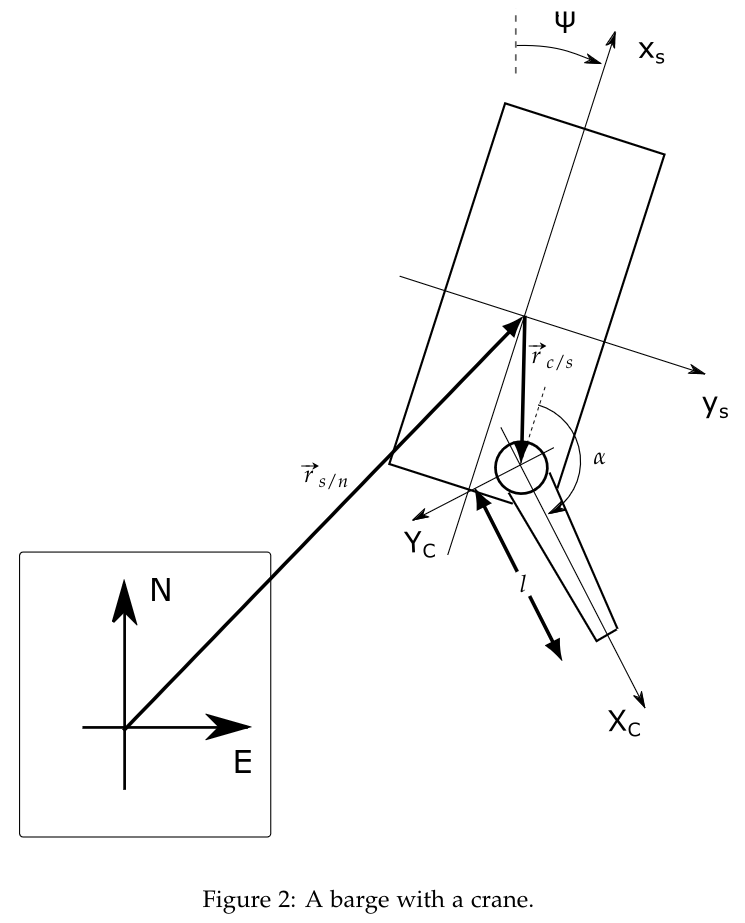And the location of the origin of the s-frame relative to the origin of the NED-frame is given as

The position of the barge is given as

$${\vec{r}}_{c/s}=a{\vec{i}}_s+b{\vec{j}}_s+c{\vec{k}}_s$$

The angle between the $x_s$-axis and the $x_c$-axis is $\alpha$, and the distance from the origin of the crane-fixed frame to the tip of the crane is $l$.

a) We want to find ${\vec{r}}_{s/n}$ expressed in terms of the s-frame.

We know that ${\vec{r}}_{s/n}=n{\vec{i}}_n+e{\vec{j}}_n+d{\vec{k}}_n$, and we now need to express ${\vec{i}}_n$, ${\vec{j}}_n$ and ${\vec{k}}_n$ in terms of ${\vec{i}}_s$, ${\vec{j}}_s$ and ${\vec{k}}_s$.

Since we found the rotation matrix in problem 1, we can find the Rotation Transformation

$$R_s^n(\psi )R_n^s(\psi )=\mathbb{I}$$

Where

$$\begin{array}{rl}{R}_n^s(\psi )& =(R_s^n(\psi ){)}^T\\ R_n^s(\psi )& =\left[\begin{array}{cc}\cos \psi & \sin \psi \\ -\sin \psi & \cos \psi \end{array}\right]\end{array}$$

We can therefore write ${\vec{r}}_{s/n}$ as

$$\begin{array}{rl}{\vec{r}}_{s/n}^s& =R_n^s(\psi ){\vec{r}}_{s/n}^n=\left[\begin{array}{ccc}\cos \psi & \sin \psi & 0\\ -\sin \psi & \cos \psi & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}n\\ e\\ d\end{array}\right]\\ {\vec{r}}_{s/n}^s& =\left[\begin{array}{c}n\cos \psi +e\sin \psi \\ -n\sin \psi +e\cos \psi \\ d\end{array}\right]\end{array}$$

b) The crane reference frame (c-frame) relative to the barge reference frame (s-frame) is given by

$${\vec{r}}_{c/s}=a{\vec{i}}_s+b{\vec{j}}_s+c{\vec{k}}_s$$

We also have a rotation around the z-axis, given by

$${\mathbf{R}}_z({\alpha }^{\prime })=\left[\begin{array}{ccc}\cos {\alpha }^{\prime }& -\sin {\alpha }^{\prime }& 0\\ \sin {\alpha }^{\prime }& \cos {\alpha }^{\prime }& 0\\ 0& 0& 1\end{array}\right]$$

Where ${\alpha }^{\prime }=\alpha$.

The resulting vector from the the origin of the s-frame to the tip of the crane, $T$, is then

$$\begin{array}{rl}{\vec{r}}_{T/s}^s& ={\vec{r}}_{c/s}^s+{\vec{r}}_{T/c}^s\\ {\vec{r}}_{T/s}^s& =a{\vec{i}}_s+b{\vec{j}}_s+c{\vec{k}}_s+l{R}_z\left(\alpha -\frac{\pi }{2}\right)\\ {\vec{r}}_{T/s}^s& =\left[\begin{array}{c}a\\ b\\ c\end{array}\right]+\left[\begin{array}{ccc}\cos \alpha & -\sin \alpha & 0\\ \sin \alpha & \cos \alpha & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}l\\ 0\\ 0\end{array}\right]\\ {\vec{r}}_{T/s}^s& =\left[\begin{array}{c}a+l\cos \alpha \\ b+l\sin \alpha \\ c\end{array}\right]\end{array}$$

c) We want to find the position of $T$ relative to the n-frame.

$$\begin{array}{r}{\vec{r}}_{T/n}^n={\vec{r}}_{s/n}^n+{\vec{r}}_{T/s}^n\end{array}$$

Where

$$\begin{array}{rl}{\vec{r}}_{T/s}^n& =R_s^n(\psi )r_{T/s}^s\\ {\vec{r}}_{T/s}^n& =\left[\begin{array}{ccc}\cos \psi & -\sin \psi & 0\\ \sin \psi & \cos \psi & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}a+l\cos \alpha \\ b+l\sin \alpha \\ c\end{array}\right]\\ {\vec{r}}_{T/s}^n& =\left[\begin{array}{c}a\cos \psi -b\sin \psi +l\cos (\alpha +\psi )\\ a\sin \psi +b\cos \psi +l\sin (\alpha +\psi )\\ c\end{array}\right]\end{array}$$

Which gives us

$$\begin{array}{rl}{\vec{r}}_{T/n}^n& ={\vec{r}}_{s/n}^n+{\vec{r}}_{T/s}^n\\ {\vec{r}}_{T/n}^n& =\left[\begin{array}{c}n+a\cos \psi -b\sin \psi +l\cos (\alpha +\psi )\\ e+a\sin \psi +b\cos \psi +l\sin (\alpha +\psi )\\ d+c\end{array}\right]\end{array}$$

d) Angular velocity of crane, $\dot{\theta }$, is the sum of all angular velocities.

$$\dot{\theta }=\dot{\psi }+\dot{\alpha }$$

e)

$$v_{s/n}^n=R_s^n(\psi )v_{s/n}^s=\left[\begin{array}{ccc}\cos \psi & -\sin \psi & 0\\ \sin \psi & \cos \psi & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}u\\ v\\ 0\end{array}\right]=\left[\begin{array}{c}u\cos \psi -v\sin \psi \\ u\sin \psi +v\cos \psi \\ 0\end{array}\right]$$

Where $\dot{n}=u\cos \psi -v\sin \psi$, and $\dot{e}=u\sin \psi +v\cos \psi$.

f)

$$\begin{array}{rl}{\vec{v}}_{T/n}& =\frac{d}{dt}{\vec{r}}_{T/n}=\frac{d}{dt}({\vec{r}}_{s/n}+{\vec{r}}_{c/s}+{\vec{r}}_{T/c})\\ {\vec{v}}_{T/n}& ={\vec{v}}_{s/n}+{\vec{\omega }}_{s/n}\times {\vec{r}}_{c/s}+{\vec{\omega }}_{c/n}\times {\vec{r}}_{T/c}\end{array}$$

Where

$$v_{s/n}^n=\left[\begin{array}{c}u\cos \psi -v\sin \psi \\ u\sin \psi +v\cos \psi \\ 0\end{array}\right],{\omega }_{s/n}^s=\left[\begin{array}{c}0\\ 0\\ \dot{\psi }\end{array}\right],r_{c/s}^s=\left[\begin{array}{c}a\\ b\\ c\end{array}\right]$$

We first calculate ${\vec{\omega }}_{s/n}\times {\vec{r}}_{c/s}$

$${\vec{\omega }}_{s/n}\times {\vec{r}}_{c/s}=\left|\begin{array}{ccc}{\vec{i}}_s& {\vec{j}}_s& {\vec{k}}_s\\ 0& 0& \dot{\psi }\\ a& b& c\end{array}\right|=-\dot{\psi }b{\vec{i}}_s+\dot{\psi }a{\vec{j}}_s$$

Then we calculate ${\vec{\omega }}_{c/n}\times {\vec{r}}_{T/c}$

$${\vec{\omega }}_{c/n}\times {\vec{r}}_{T/c}=\left|\begin{array}{ccc}{\vec{i}}_c& {\vec{j}}_c& {\vec{k}}_c\\ 0& 0& \dot{\alpha }\\ 1& 0& 0\end{array}\right|=\dot{\alpha }l{\vec{j}}_c$$

To calculate ${\vec{v}}_{T/n}^n$ we can solve

$${\vec{v}}_{T/n}^n={\vec{v}}_{s/n}^n+R_s^n(\psi )({\omega }_{s/n}^s\times r_{c/s}^s)+R_s^n(\psi )R_c^s(\alpha )({\omega }_{c/n}^c\times r_{T/c}^c)$$

Where

$$\begin{array}{rl}{R}_s^n(\psi )& =\left[\begin{array}{ccc}\cos \psi & -\sin \psi & 0\\ \sin \psi & \cos \psi & 0\\ 0& 0& 1\end{array}\right]\\ R_c^s(\alpha )& =\left[\begin{array}{ccc}\cos \alpha & -\sin \alpha & 0\\ \sin \alpha & \cos \alpha & 0\\ 0& 0& 1\end{array}\right]\end{array}$$

This gives us

$${\vec{v}}_{T/n}^n=\left[\begin{array}{c}u\cos \psi -v\sin \psi -\dot{\psi }b\cos \psi -\dot{\psi }a\sin \psi -\dot{\alpha }l\sin (\alpha +\psi )\\ u\sin \psi +v\cos \psi -\dot{\psi }b\sin \psi +\dot{\psi }a\cos \psi +\dot{\alpha }l\cos (\alpha +\psi )\\ 0\end{array}\right]$$

---