Realizations

If we have a Proper Transfer Function which is also rational, we can find a realization from Laplace form to State Space Representation

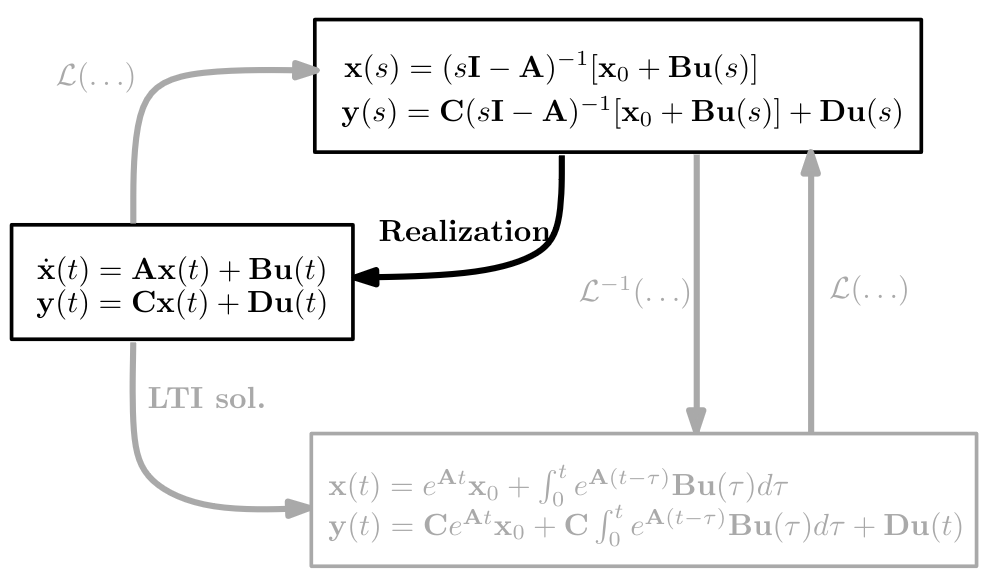
Since we can transform a system in infinite many ways using $\bar{x}=Tx$, there are also infinite many state-spaces we can realize to However it is normal to realize to a Canonical Forms

---

$$G(s)=G_{sp}(s)+G_{\infty }$$

Improper Transfer Function Proper Transfer Function Strictly Proper Transfer Functions

Matching

After finding the above, we now need to find a state-space model which we will use. It is normal to use Canonical Forms.

Example

Given the following transfer function for a mass spring damper

$$H(s)=\frac{\frac{1}{m}}{s^2+s\left(\frac{d}{m}\right)+\frac{k}{m}}$$

And since we are using the Controllable Canonical Form:

A &= \begin{bmatrix} -\alpha_{1} & -\alpha_{2} \\ 1 & 0 \end{bmatrix} \\ B &= \begin{bmatrix} 1 \\ 0 \end{bmatrix} \\ C &= \begin{bmatrix} n_{1} & n_{2} \end{bmatrix} \end{align}

Since the system is strictly proper, $G_{\infty }=0$, and we get:

$$G_{sp}(s)=C(sI-A{)}^{-1}B+G_{\infty }=\frac{s{n}_1+n_2}{s^2+s{\alpha }_1+{\alpha }_2}$$

meaning that

A &= \begin{bmatrix} -\frac{d}{m} & -\frac{k}{m} \\ 1 & 0 \end{bmatrix} \\ B &= \begin{bmatrix} 1 \\ 0 \end{bmatrix} \\ C &= \begin{bmatrix} 0 & \frac{1}{m} \end{bmatrix} \end{align}