Assignment 5 - Lagrange 1

In this assignment we will study the modeling of complex mechanical systems based on the Lagrange approach.

---

Problem 1 (Ball on a Beam)

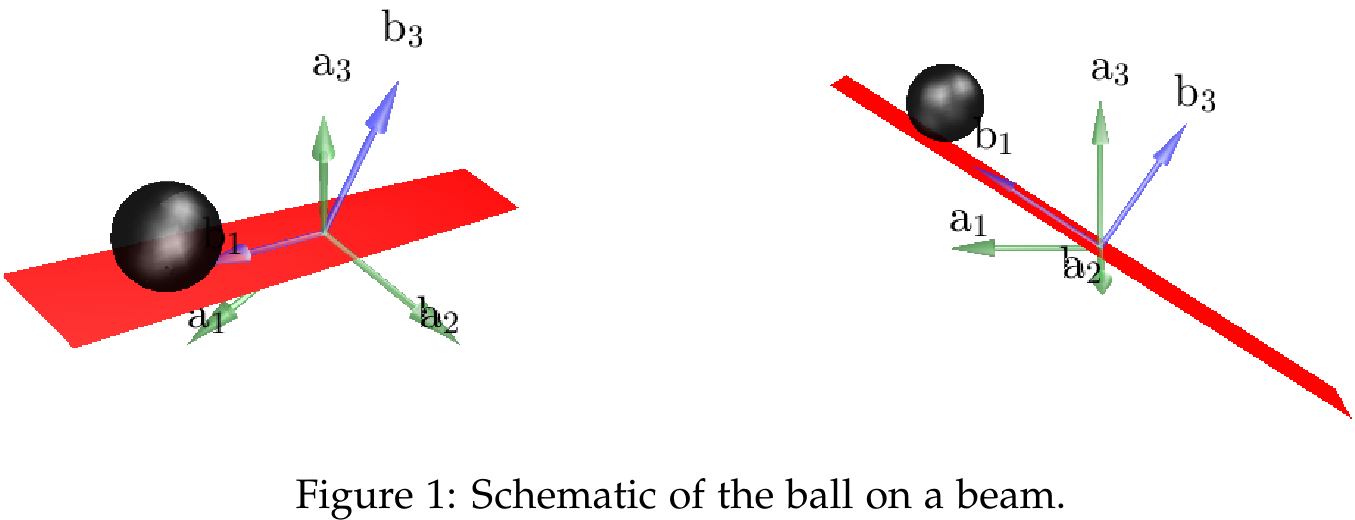We will use the Generalized Coordinates $\mathbf{q}=[x,\theta {]}^T$.

a)

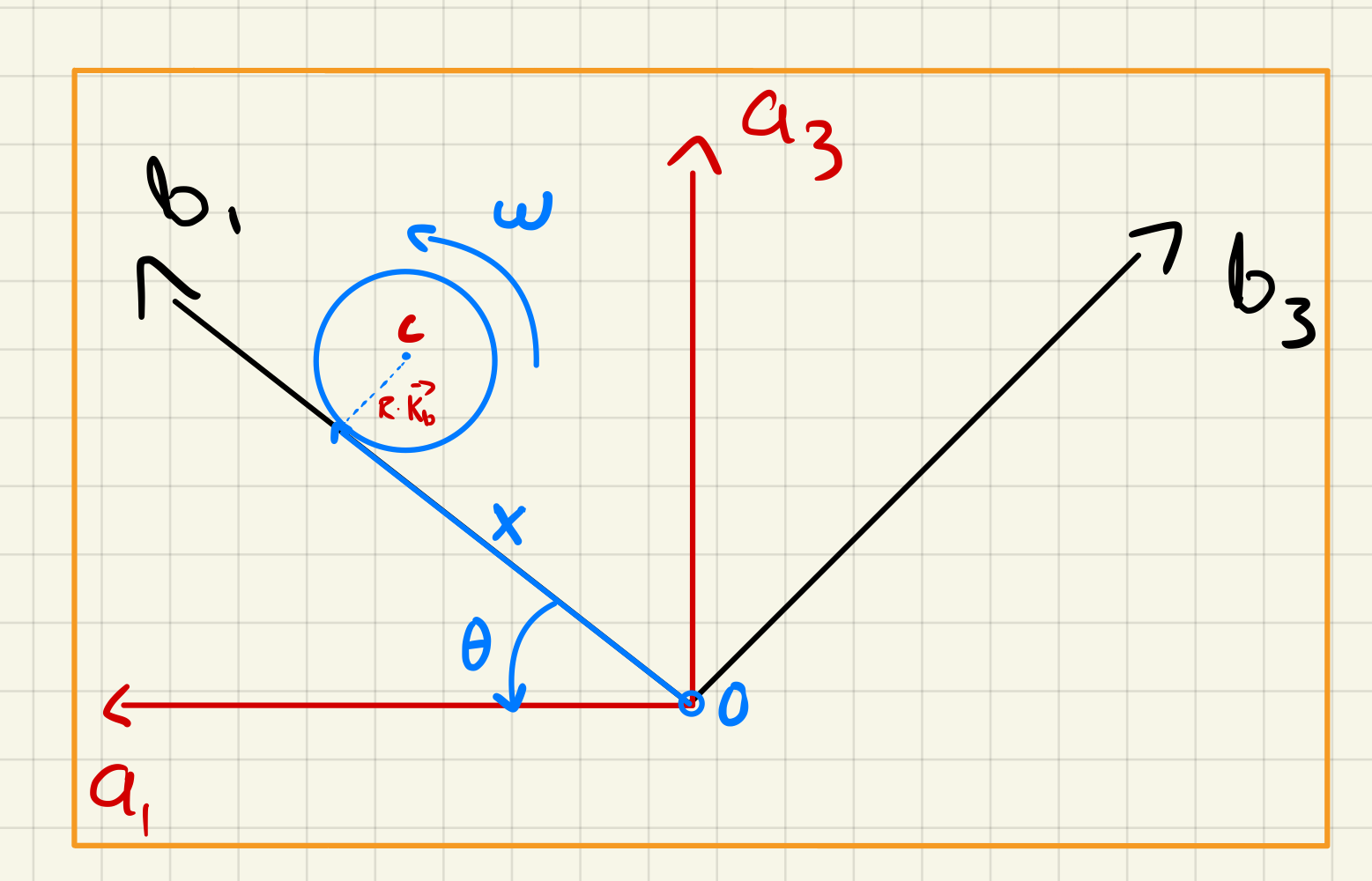The position of the ball’s center as a function in the $a$-frame, of the generalized coordinates can be expressed as

$$\begin{array}{rl}{\vec{r}}_{M/b}^a& =\underset{R_y(-\theta )}{\underbrace{R_b^a}}{\vec{r}}_{M/b}^b\\ {\vec{r}}_{M/b}^a& =\left[\begin{array}{ccc}\cos \theta & 0& -\sin \theta \\ 0& 1& 0\\ \sin \theta & 0& \cos \theta \end{array}\right]\left[\begin{array}{c}x\\ 0\\ R\end{array}\right]\\ {\vec{r}}_{M/b}^a& =x\left[\begin{array}{c}\cos \theta \\ 0\\ \sin \theta \end{array}\right]+R\left[\begin{array}{c}-\sin \theta \\ 0\\ R\cos \theta \end{array}\right]\end{array}$$

b)

Rolling gives

$${\omega }_{M/b}^b=\left[\begin{array}{c}0\\ \dot{x}/R\\ 0\end{array}\right]$$

Tilting the beam gives

$${\omega }_{b/a}^b=\left[\begin{array}{c}0\\ \dot{\theta }\\ 0\end{array}\right]$$

In total this gives

$${\omega }_{M/a}^a=\left[\begin{array}{c}0\\ \dot{x}/R+\dot{\theta }\\ 0\end{array}\right]$$

c)

We have both kinetic energy due to translation

Link to original

Where $\dot{p}$ is given by

$$\dot{p}=\dot{x}\left[\begin{array}{c}\cos \theta \\ 0\\ \sin \theta \end{array}\right]+x\left[\begin{array}{c}-\sin \theta \\ 0\\ \cos \theta \end{array}\right]\dot{\theta }+R\left[\begin{array}{c}-\cos \theta \\ 0\\ -\sin \theta \end{array}\right]\dot{\theta }$$

Giving us

$$T_T=\frac{1}{2}{\dot{q}}^T\left[\begin{array}{cc}m& 0\\ 0& m(x^2+R^2)\end{array}\right]\dot{q}$$

And kinetic energy due to the rotation is given by

$$\begin{array}{rl}{T}_{rot}& =\frac{1}{2}\underset{\frac{2}{5}M{R}^2\mathbb{I}}{\underbrace{I_{ball}}}\underset{(\dot{\theta }+\dot{x}/R{)}^2}{\underbrace{{\omega }^2}}\end{array}$$

So the ball has kinetic energy

$$T_{ball}=T_T+T_{rot}$$

d)

The kinetic energy of the beam is

$$T_{beam}=\frac{1}{2}({\omega }_{b/a}^a{)}^{T}J{\omega }_{b/a}^a=\frac{1}{2}J{\dot{\theta }}^2,J=1$$

e)

The following changes in BallAndBeamSimulation.m

We find the Generalized Forces, $Q$

$$Q=[0,T{]}^T$$

Where $T$ is the torque

.
.
.
% Define symbolic variable q for the generalized coordinates
% x and theta
q  = [x; theta];
% Define symbolic variable dq for the derivatives 
% of the generalized coordinates
dq = [dx; dtheta];
% Write the expressions for the position of
% the center of the ball:
p = [
    x*cos(theta)-R*sin(theta);
    0;
    x*sin(theta) + R*cos(theta)
    ];   
             
% Kinetic energy
T = 1/2*J*dtheta^2; % kinetic energy of beam
 
dp = jacobian(p,q)*dq; % linear velocity of ball
T  = T + 1/2*M*(dp.')*dp; % add linear kinetic energy of ball
 
I     = 2/5*M*R^2*eye(3); % inertia in rotation of ball
omega = [0; dx/R+dtheta; 0]; % angular velocity of ball
 
T  = T + 1/2 *(omega.')*I*omega; % add rotational kinetic energy of ball
 
T = simplify(T);
 
% Potential energy
V = M*g*p(3);
 
% Generalized forces
Q = [0; -To];
 
% Lagrangian
Lag = T-V;
.
.
.

f)

We assume that the external torque $T$ is given by the PD control law

$$T=200(x-\theta )+70(\dot{x}-\dot{\theta })$$

Idk how to do this task

Problem 2 (Pendulum on an Oscillator)

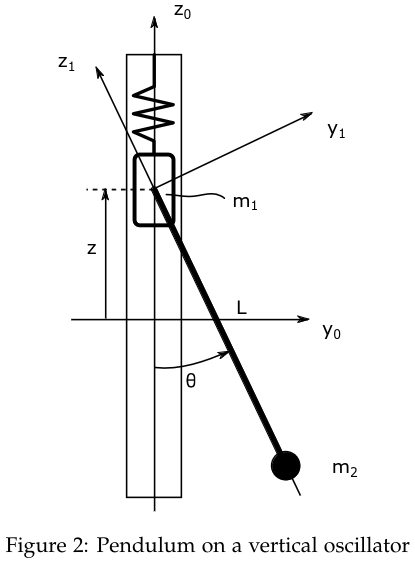
a)

We set

$$q=\left[\begin{array}{c}z\\ \theta \end{array}\right]$$

b)

The kinetic energy is given by

$$T=\underset{\text{Translation of }{M}_1}{\underbrace{\frac{1}{2}{m}_1{\dot{z}}^2}}+\underset{\text{Translation of pendulum axis}}{\underbrace{\frac{1}{2}{m}_2{\dot{z}}^2}}+\underset{\text{Pendulum Rotation}}{\underbrace{\frac{1}{2}{m}_2{L}^2{\dot{\theta }}^2}}$$

c)

The potential energy of the system is given by

$$V=\underset{\text{Spring}}{\underbrace{\frac{1}{2}k{z}^2}}+\underset{\text{Gravity force of pendulum}}{\underbrace{\frac{1}{2}{m}_{2}gL(1-\cos \theta )}}$$

d)

We have

Link to original

Where

The Lagrange functions is defined as $\mathcal{L}(q,\dot{q})=T(q,\dot{q})-V(q)\in \mathbb{R}$ Where $T(q,\dot{q})$ is the Kinetic Energy, and $V(q)$ is the Potential Energy.

Link to original

Which gives

$$\begin{array}{rl}\frac{d}{dt}\frac{\partial L}{\partial \dot{q}}& =\frac{d}{dt}[(m_1+m_2)\dot{z},m_2{L}^2\dot{\theta }]=[(m_1+m_2)\ddot{z},m_2{L}^2\ddot{\theta }]\end{array}$$

And

$$\frac{\partial L}{\partial q}=\left[-kz,-\frac{1}{2}{m}_{2}gL\sin \theta \right]$$

Which gives

$$\begin{array}{rl}\ddot{z}& =-\frac{k}{m_1+m_2}z\\ \ddot{\theta }& =\frac{-g\sin \theta }{2L}\end{array}$$