Assignment 6

Resources: 6.1, 7.1, 7.1.2, 7.2.1, 7.3.1, 7.4, 8.1.3

Problem 1

Given the following sequence of length $N_x$

$$x(n)=\{\begin{array}{l}0.9^{n}n=0,1,\dots N_x-1\\ 0otherwise\end{array}$$

Where $N_x=28$

a)

DTFT - Discrete Time Fourier Transform

DTFT is a way of looking at the signal in the frequency domain. The formula is given by $X(\omega )={\sum }_{n=-\infty }^{\infty }x[n]e^{-j\omega n}$

Link to original

We can now compute $X(\omega )=X(2\pi f)$ using the formula for a finite geometric series

---

Finite Geometric Series

$$\sum _{k=0}^{n-1}a{r}^k=\sum _{k=1}^{n}a{r}^{k-1}=\{\begin{array}{l}a\left(\frac{1-r^n}{1-r}\right)r\ne 1\\ anr=1\end{array}$$Link to original

---

X(\omega)&= \sum_{n=0}^{N_{x}-1}0.9^ne^{-j\omega n} \\ X(\omega)&= \sum_{n=0}^{N_{x}-1}(0.9e^{-j\omega})^n \\ X(\omega)&= \frac{1-(0.9e^{-j\omega})^{N_{x}}}{1-0.9e^{-j\omega}} \end{align}

b)

c) The relationship is given by

$$f=\frac{k}{N},k=0,\dots ,N-1$$

where $N$ is the number of points.

d) After plotting, we can clearly see that the DFT-values are not accurate when the number of samples for the DFT are too small. In this case, $N_x$.

e) Since real discrete values signals are unique only for $-\frac{1}{2}<f<\frac{1}{2}$, we only care about values in this range. However, due to the symmetrical properties of the DTFT and DFT, it is symmetrical around $0$, therefore we only need to look at the frequency range $0<f<\frac{1}{2}$.

Problem 2

Given the following sequence of length $N_h=9$

$$x(n)=\{\begin{array}{ll}1& n=0,1,\dots N_h-1\\ 0& \text{ce}otherwise\end{array}$$

a) The length of a convolution between a signal $x[n]$ (with length $N_x$), and a filter $h[n]$ (with length $N_h$), is given by

$$N_y=N_x+N_h-1=36$$

Which is the same as the plot

b) To avoid Time Domain Aliasing we need the length of the DFT to be atleast equal to $N_y$. This is shown through the following figure.

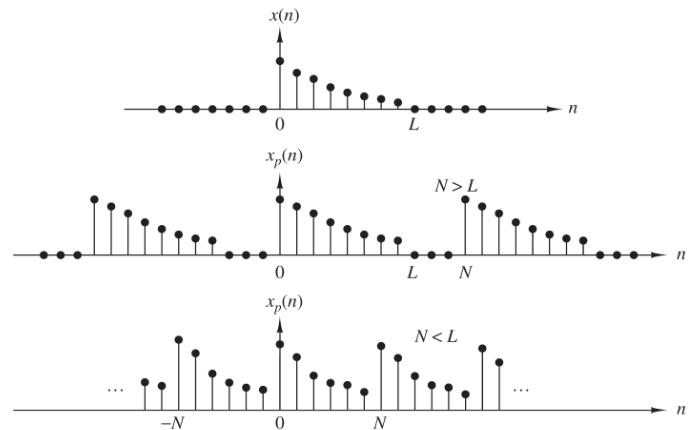
Problem 3

Problem 4

a) The Fast Fourier Transform is a more computationally efficient way of computing the DFT. There are several algorithms that does this.

b) The Radix-2 FFT is an algorithm that can be used when $N=2^{\nu }$, and we can use zero padding to achieve the correct number of points. Using a divide and conquer algorithm that uses the symmetric properties of the window function. It reduces the runtime from $\Theta (N^2)$ to $\Theta (Nl{g}_2(N))$.

c) Solving directly gives us

Link to original

Which has a runtime of $\Theta (n^2)$

d)