Chapter 12 - Linear Prediction and Optimum Linear Filters

Resources: page=845

12.2 - Innovations Representation of a Stationary Random Process

Resources: page=857

Idea: A random Wide-sense stationary process can be represented as the output of a causal and causally invertible linear system excited by a white noise process.

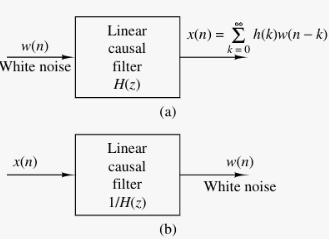
Here, $\frac{1}{H(z)}$ is called a noise whitening filter, and its output, $w(n)$ is called the innovations process associated with the stationary random process $x(n)$.

---

12.2.1 Rational Power Spectra

Given that ${\Gamma }_{xx}$ is a rational function, and the Power Density Spectrum (PDS) of a random process, $x(n)$, and that the roots of $A(z)$ and $B(z)$ fall inside the unit circle, then we can express $H(z)$ in the following way:

$$H(z)=\frac{B(z)}{A(z)}=\frac{{\sum }_{k=0}^q{b}_k{z}^{-k}}{1+{\sum }_{k=1}^p{a}_k{z}^{-k}},|z|>r_1$$

Where $b_k$ is the filter coefficients that determines the location of the zeros, and $a_k$ determines the location for the poles.

$H(z)$ is a causal, stable and Minimum-Phase linear system.

This gives us

$$x(n)+\sum _{k=1}^p{a}_{k}x(n-k)=\sum _{k=0}^q{b}_{k}w(n-k)$$

These are the three specific cases we distinguish between depending on the values of $a_k$ and $b_k$:

---

Autoregressive (AR) Process

---

Moving Average (MA) process

---

Autoregressive, Moving Average (ARMA) process

---

12.2.2 Relationships Between the Filter Parameters and the Autocorrelation Sequence

We can write the stochastic Autocorrelation of $x[n]$ as

$${\gamma }_{xx}(m)=-\sum _{k=1}^p{a}_k{\gamma }_{xx}(m-k)+\sum _{k=0}^q{b}_k{\gamma }_{wx}(m-k)$$

Where ${\gamma }_{wx}(m)$ is the Crosscorrelation sequence between $w[n]$ and $x[n]$ at lag $m$.

$${\gamma }_{wx}=\cdots =\{\begin{array}{ll}0,& m>0\\ {\sigma }_w^{2}h(-m),& m\le 0\end{array}$$

Giving us the following equation for a general Autoregressive, Moving Average (ARMA) process.

$${\gamma }_{xx}=\{\begin{array}{ll}-{\sum }_{k=1}^p{a}_k{\gamma }_{xx}(m-k),& m>0\\ -{\sum }_{k=1}^p{a}_{k{\gamma }_{xx}}(m-k)+{\sigma }_w^2{\sum }_{k=0}^{q-m}h(k)b_{k+m},& m=0\\ {\gamma }_{xx}^{\ast }(-m),& m<0\end{array}$$

This is very important, as we now have a linear relationship between $y_{xx}(m)$ and $a_k$. We can now use the Yule-Walker equations

The simultaneous joint probability density function can be shifted in time if the statistical properties of the process does not depend on time. If the process is stationary, then $R_x(t_1,t_2)=E[X(t_1)X(t_2)]$ reduces to

Transclude of Autocorrelation#^fc34ea