New Lagrangian

$$L(q,\dot{q})=T(q,\dot{q})-V(q)-z^{T}c(q)$$

Where $z$ are the Lagrangian multipliers, and $c(q)$ are a set of constraint equations.

Lagrange Equation

---

Note

The equations of motion is still $\frac{d}{dt}\left(\frac{\partial L}{\partial q}\right)-\frac{\partial L}{\partial q}=Q$ With $\ddot{c}(q,\dot{q},\ddot{q})=0$

It is easier to solve the system if $\ddot{q}$ appears in the constraint

$$c(q)=0\leftrightarrow \ddot{c}=0,\{\begin{array}{l}c(0)=0\\ \dot{c}(0)=0\end{array}$$

Examples

Pendulum without $\theta$

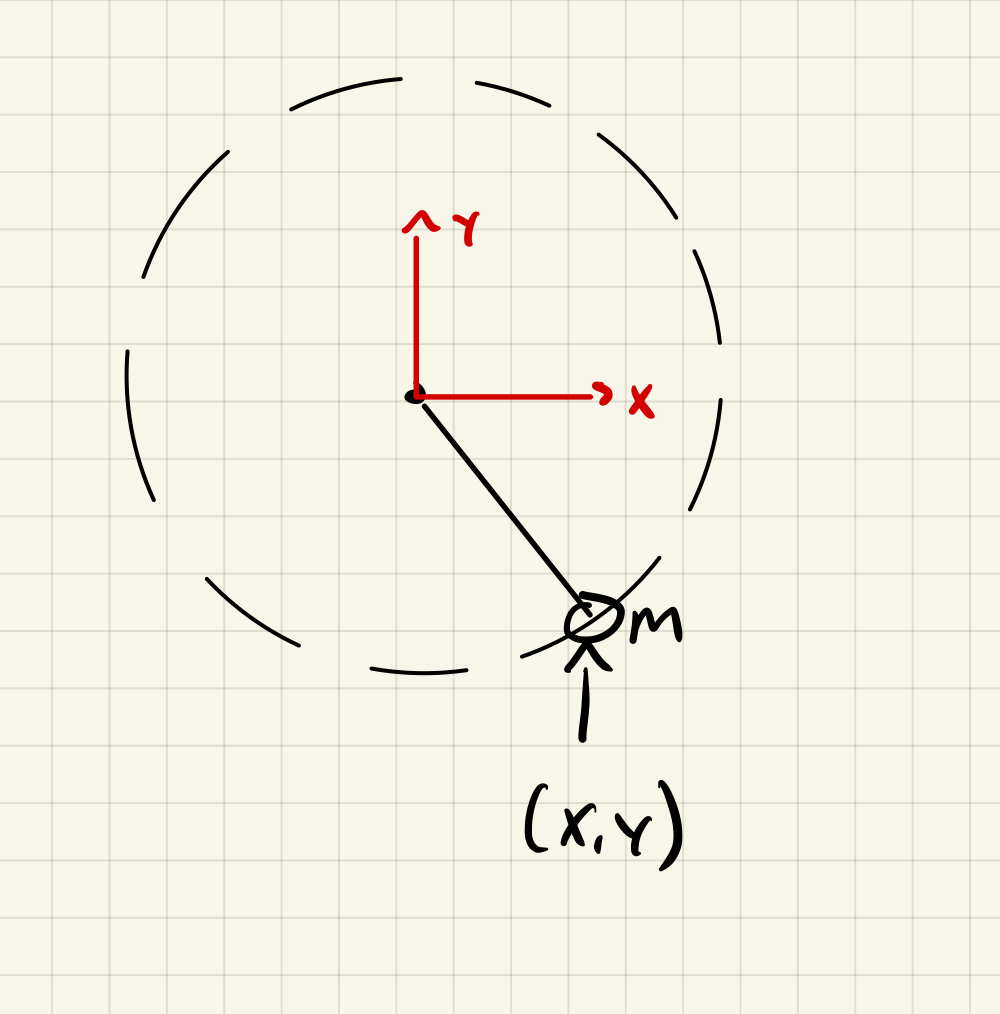We have the Generalized Coordinates, $q=[x,y{]}^T$, the number of coordinates, $M=2$, and the degrees of freedom, $N=1$.

$$\begin{array}{rlr}m\ddot{x}& =Q_x& \\ m\ddot{y}& =Q_y,& \text{We need constraint here to keep the model intact}\end{array}$$

The constraints then becomes

$$c(q)=\frac{1}{2}(x^2+y^2-L^2)=0$$

We get the Kinetic Energy

$$T=\frac{1}{2}m({\dot{x}}^2+{\dot{y}}^2)$$

And the Potential Energy equal to zero (since we assume rotation on flat surface)

$$V=0$$

Then the New Lagrangian becomes

$$L=T-V-z^{T}c(q)=\frac{1}{2}m({\dot{x}}^2+{\dot{y}}^2)-0-\frac{1}{2}z(x^2+y^2-L^2)$$

We now start solving the components needed for the Euler-Lagrange Equation

$$\begin{array}{rl}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right)& =m\ddot{x}\\ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{y}}\right)& =m\ddot{y}\\ \frac{\partial L}{\partial x}& =-zx\\ \frac{\partial L}{\partial y}& =-zy\\ \dot{c}(q,\dot{q})& =x\dot{x}+y\dot{y}\\ \ddot{c}(q,\dot{q},\ddot{q})& =x\ddot{x}+y\ddot{y}+{\dot{x}}^2+{\dot{y}}^2\end{array}$$

We can now solve the Euler-Lagrange Equation, which is

Link to original

$$\begin{array}{rl}\left[\begin{array}{cc}m& 0\\ 0& m\end{array}\right]\left[\begin{array}{c}\ddot{x}\\ \ddot{y}\end{array}\right]+\left[\begin{array}{c}zx\\ zy\end{array}\right]& =\left[\begin{array}{c}0\\ 0\end{array}\right]\\ & \text{And}\\ x\ddot{x}+y\ddot{y}& =-{\dot{x}}^2-{\dot{y}}^2\end{array}$$

Giving us

$$\begin{array}{rl}\left[\begin{array}{ccc}m& 0& x\\ 0& m& y\\ x& y& 0\end{array}\right]\left[\begin{array}{c}\ddot{x}\\ \ddot{y}\\ z\end{array}\right]& =\left[\begin{array}{c}0\\ 0\\ -{\dot{x}}^2-{\dot{y}}^2\end{array}\right]\end{array}$$

Finally giving us

$$\begin{array}{rl}\left[\begin{array}{c}\ddot{x}\\ \ddot{y}\\ z\end{array}\right]& =\frac{1}{m(x^2+y^2)}\left[\begin{array}{ccc}{y}^2& -xy& mx\\ -xy& x^2& my\\ mx& my& -m^2\end{array}\right]\left[\begin{array}{c}0\\ 0\\ -{\dot{x}}^2-{\dot{y}}^2\end{array}\right]\end{array}$$

Where we have $L=x^2+y^2$.