Radix-2 FFT

An algorithm to solve the FFT- Fast Fourier Transform.

---

How it works

Radix-2 FFT Algorithms

Dividing the DFT - Discrete Fourier Transform problem into smaller successively smaller DFTs, then solving recursively.

X(k)&=\sum^{N-1}_{n=0}x[n]e^{-jw\pi nk/N} \\ X(k)&=\sum_{n=0}^{N-1}x[n]W^{nk}_{N} \end{align}

We do this by exploiting the symmetry and periodicity of $W_N^{nk}$

W_{N}^{k+N} &=e^{-j2\pi(k+N)/N}=W_{N}^k \\ W_{N}^{k+N/2} &=e^{-j2\pi(k+N/2)/N}=-W_{N}^k \\ W_{N}^{2k} &=e^{-j2\pi k/(N/2)}=W_{N/2}^k \end{align}

Now, if we assume that $N=2^{\nu }$, and split our signal, $x[n]$ into even and odd numbers:

f_{1}[n] &= x[2n] \\ f_{2}[n] &= x[2n+1] \end{align}

We can split our DFT into both odd and even values of $n$.

X(k) &= \sum_{\ce{ n even }}x[n]W_{N}^{nk} +\sum_{\ce{ n odd }}x[n]W^{nk}_{N} \\ X(k) &=\sum_{m=0}^{N/2-1}x[2m]W_{N}^{2mk}+\sum_{m=0}^{N/2-1}x[2m+1]W_{N}^{(2m+1)k} \end{align}

Which is the same as

$$\begin{array}{rl}X(k)& =\sum _{m=0}^{N/2-1}{f}_1[m]W_{N/2}^{mk}+W_N^k\sum _{m=0}^{N/2-1}{f}_2[m]W_{N/2}^{mk}\end{array}$$

For $k=0,\dots ,N-1$.

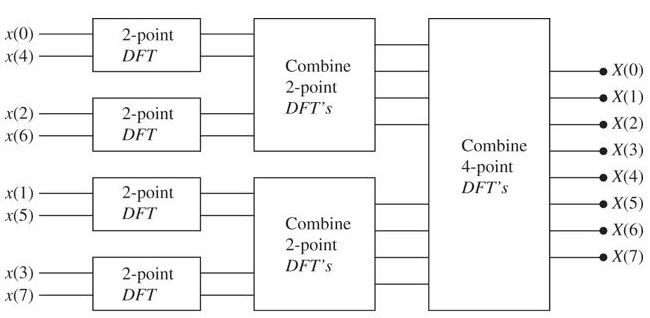
We have now reduced the problem into two subproblems of size $N/2$. Since $F_1={\sum }_{m=0}^{N/2-1}{f}_1[m]W_{N/2}^{mk}$ and $F_2={\sum }_{m=0}^{N/2-1}{f}_2[m]W_{N/2}^{mk}$ are periodic (?), $X(k)$ is also periodic. This reduces the number of operations to

$$T(N)=2{\left(\frac{N}{2}\right)}^2+\frac{N}{2}$$

If we continue doing this, aka dividing in two again and again

$$\begin{array}{rl}N& =2^{\nu }\\ \nu & ={\log }_{2}N\end{array}$$

We can reduce the problem ${\log }_{2}N$ times, giving us a total computational complexity of

\frac{N}{2}\log_{2}N \; \; \ce{multiplications } \\ N\log_{2}N \; \; \ce{ Additions } \end{align}

This gives us a final model which does the computations as an In-Place Algorithm Runtime - $\Theta (Nl{g}_{2}N)$

Link to original