Exercise 7 - Riccati Equation and State Estimation

Given the following second-order system

$$\ddot{x}+k_1\dot{x}+k_{2}x=k_{3}u$$

In continuous State Space Representation form, with $x_1=x$ and $x_2=\dot{x}$ we get

$$\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\end{array}\right]=\underset{A_c}{\underbrace{\left[\begin{array}{cc}0& 1\\ -k_2& -k_1\end{array}\right]}}\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]+\underset{B_c}{\underbrace{\left[\begin{array}{c}0\\ k_3\end{array}\right]}}u$$

In discrete form using Euler Discretization

$$x_{t+1}=\underset{A}{\underbrace{\left[\begin{array}{cc}1& T\\ -k_{2}T& 1-k_{1}T\end{array}\right]}}{x}_t+\underset{B}{\underbrace{\left[\begin{array}{c}0\\ k_{3}T\end{array}\right]}}{u}_t$$

We set $k_1=k_2=k_3=1$ and $T=0.1$ with initial condition $x_0=[5,1{]}^T$, and the initial state estimate is ${\hat{x}}_0=[6,0{]}^T$ when an observer is used

Problem 1 (20%) The Riccati Equation

Algebraic Ricatti Equation

Matrix Inversion Lemma

$$(S+UTV{)}^{-1}=S^{-1}-S^{-1}U(T^{-1}+V{S}^{-1}U{)}^{-1}V{S}^{-1}$$Link to original

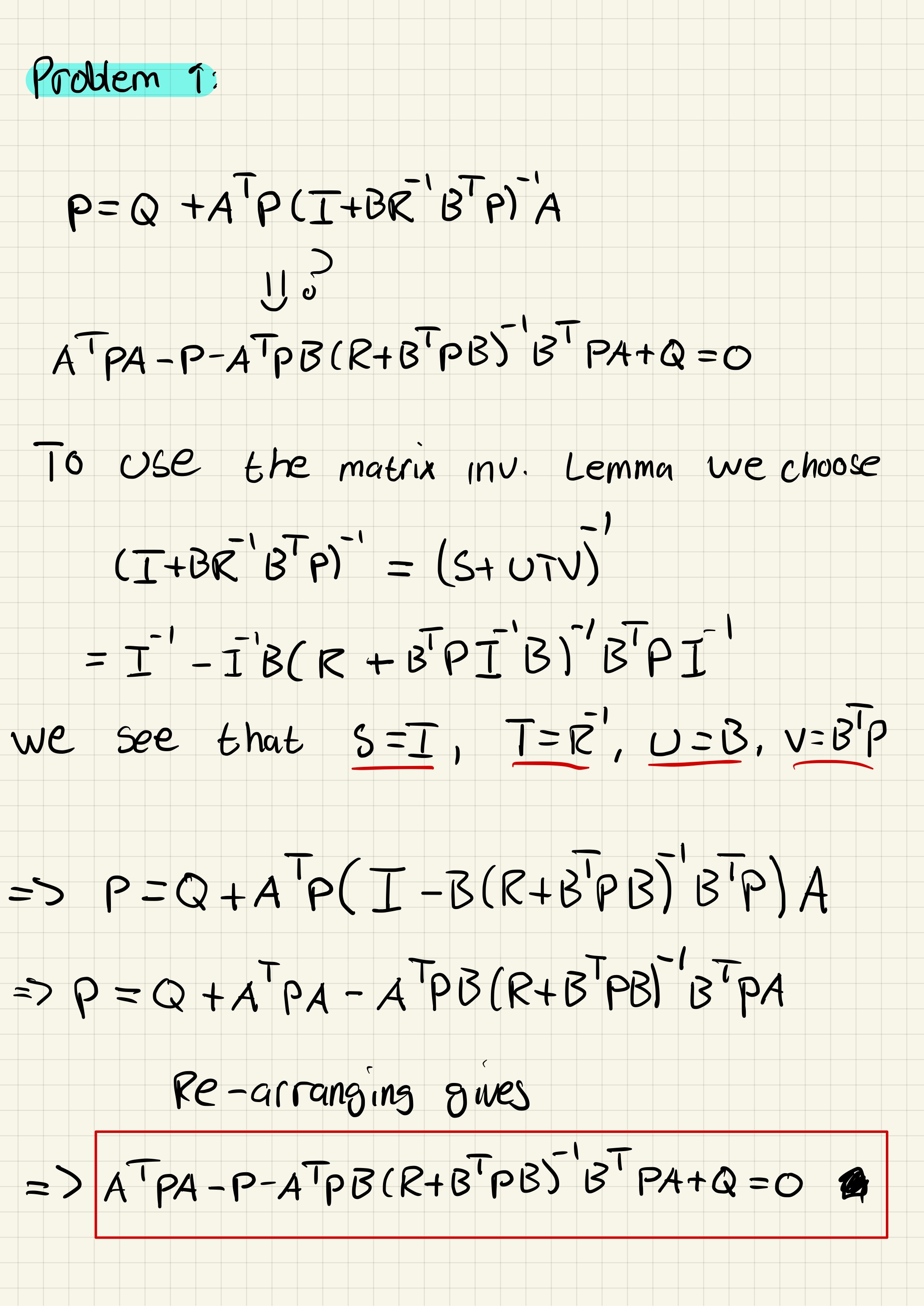
Problem 2 (30%) LQR and State Estimation

We only measure $x_1$

$$y_t=\underset{C}{\underbrace{\left[\begin{array}{cc}1& 0\end{array}\right]}}{x}_t$$

And we use LQR and an observer to control the output.

a)

The following Matlab script find the optimal feedback gain $K$ assuming that the full state is available for feedback

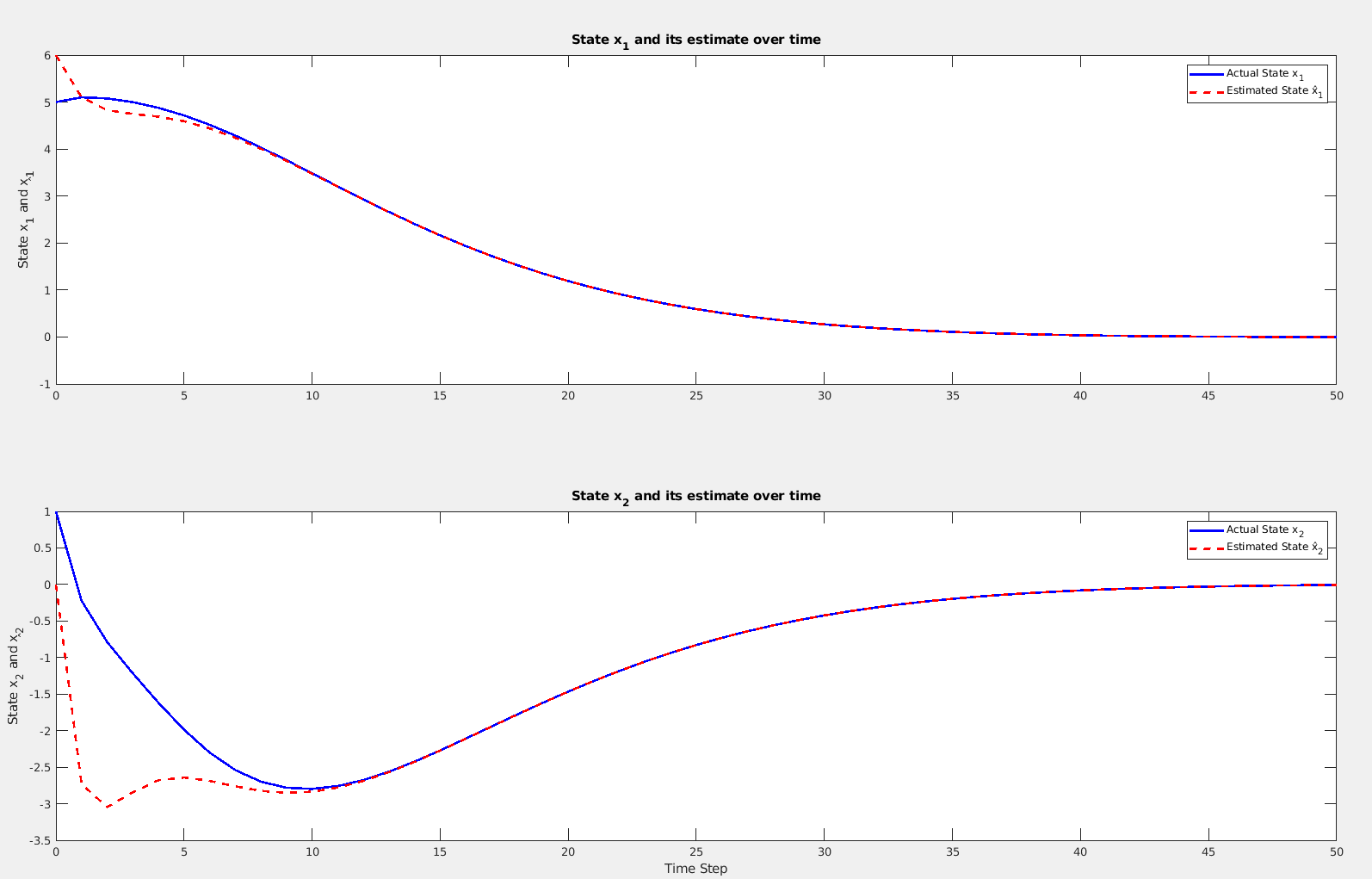
 Plot
% Adjust the time vector to exactly match the state vectors' length
time_vector = 0:final_time;
 
% Ensure the plot commands only include vectors of the same length
% Since x and x_hat include the initial state, we plot them directly against the time vector
 
% Plotting
figure;
 
% Plot actual state x
subplot(2,1,1); % Create subplot for the first state
plot(time_vector, x(1,:), 'b-', 'LineWidth', 2); hold on; % Plot first state over time
plot(time_vector, x_hat(1,:), 'r--', 'LineWidth', 2); hold off; % Plot first estimated state over time
ylabel('State x_1 and x̂_1');
legend('Actual State x_1', 'Estimated State x̂_1');
title('State x_1 and its estimate over time');
 
subplot(2,1,2); % Create subplot for the second state
plot(time_vector, x(2,:), 'b-', 'LineWidth', 2); hold on; % Plot second state over time
plot(time_vector, x_hat(2,:), 'r--', 'LineWidth', 2); hold off; % Plot second estimated state over time
ylabel('State x_2 and x̂_2');
legend('Actual State x_2', 'Estimated State x̂_2');
title('State x_2 and its estimate over time');
 
xlabel('Time Step');

Gave me this figure

c)

The following

phi = [A-B*K B*K;
       zeros(size(A)) A-K_F*C];
 
eig(phi)

Gave me the eigenvalues

ans =
 
   0.8675 + 0.0531i
   0.8675 - 0.0531i
   0.5000 + 0.0300i
   0.5000 - 0.0300i

Which is the eigenvalues of both the system in closed loop, and the observer.

Problem 3 (30%) MPC and State Estimation

We now add the input constraint

$$-4\le u_t\le 4,t=1,\dots ,N-1$$

And use MPC with

$$Q=\left[\begin{array}{cc}4& 0\\ 0& 4\end{array}\right],R=1$$

a)

Problem 4 (20%) Infinite-Horizon MPC

I realize that this might not be enough to get the assignment approved, but I was pretty demotivated to do all of this Matlab scripting in one assignment.