Dynamisk programmering

page=482 En metode å designe Algoritme - Algorithms på som gjør de mye mer effektive, som vi kan benytte dersom vi har visse egenskaper ved problemet vårt:

• Optimal Delstruktur

  En optimal løsning på problemer består av å lage optimal løsninger av mindre delproblemer

  ---

  Link to original

• Overlappende Delinstanser

  Støter på samme delproblemene gjentatte ganger, og at disse blir beregnet unødvendig mange ganger ved en Naiv Algoritme.

  Link to original

Problemer

Cut-Rod

Problemstilling

Cut-Rod handler om at du har en stokk med lengde cm og en tabell med priser $p=[p_1,\dots ,p_n]$, hvor $p_i$ angir prisen til en stokk med lengde $i$ cm. Vi ønsker å kappe opp denne stokken slik at total pris maksimeres (vi kan kun kappe på hvert heltall antall cm). Det er totalt $2^{n-1}$ forskjellige måter å kutte opp en stokk på $n$ cm, da vi har $n-1$ indre punkter å kutte på ($1,2,\dots ,n-1$), og på hver av punktene er valget binært; kutt eller ikke kutt.

Eksempel: Vi er gitt tabellen under og $n=4$. Da har vi $2^{4-1}=8$ mulige oppkuttinger. Vi må finne ut hvilken av disse 8 mulighetene som gir maksimal pris. Den naive løsningen (Naiv Algoritme) er å sjekke alle 8 kombinasjoner og sammenligne disse, men da må vi i så fall sjekke eksponentielt mange kombinasjoner - ikke bra! En naiv løsning er presentert i algoritmen Cut-Rod.

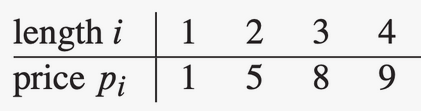
Naiv løsning

Gitt en liste som sier noe om hvor mye ulike lengder er verdt Da har vi 5 måter å gjøre det første kuttet på 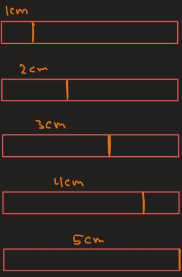Etter vi har gjort det første kuttet får vi en resterende del, men vi antar at den allerede er kuttet opp på en optimal måte.

Da blir vi møtt med følgende alternativer for hva det meste vi kan tjene på stangen:

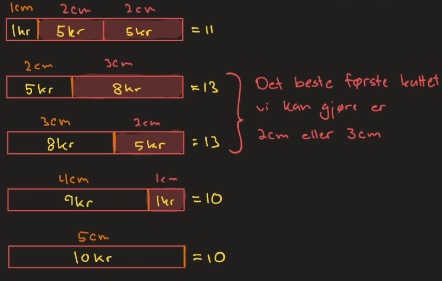
Vi må derimot faktisk løse delproblemene selv

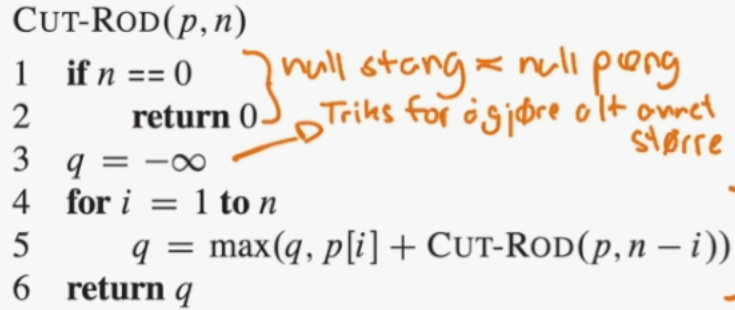
Memoisering (top down) løsning

Den naive løsningen regner samme verdier flere ganger. I denne løsningen sjekker vi i hvert rekursjonskall om delinstansen har blitt regnet ut fra før av før man foretar beregningen.

Kjøretid: $\Theta (n^2)$

Iterasjon (bottom up) løsning

Vi starter med minste delinstans, lagrer svaret og itererer videre over delinstansene

Kjøretid: $\Theta (n^2)$

Fordeler/Ulemper bottom up/top down

Algoritme	Fordeler	Ulemper
Bottom up	Bedre konstanter i kjøretid	Avhenger av vi kjenner størrelsen på delproblemene
Top down	Vi beregner en instans kun EN GANG	Vi bruker rekursjon → Mer overhead

LCS - longest Common Subsequence

Problem

Gitt en sekvens $X=<A,B,H,C,D,E,V>$, kan vi finne en Delsekvens (Subsequence).

LCS handler om å finne største delsekvens mellom to arrays

A &= [b,c,a,e,f] \\ B &= [a,b,c,f,e] \end{align}

Da blir $[a,f]$ og $[b,c,f]$ delsekvenser av $A$ og $B$, og $[b,c,f]$ er den lengste.

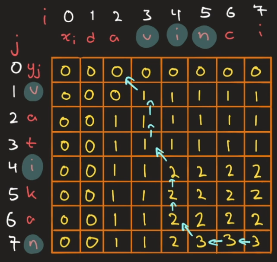Alternativt 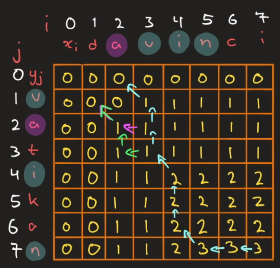Og ser typisk slik ut på eksamen: Kjøretid: $\Theta (mn)$