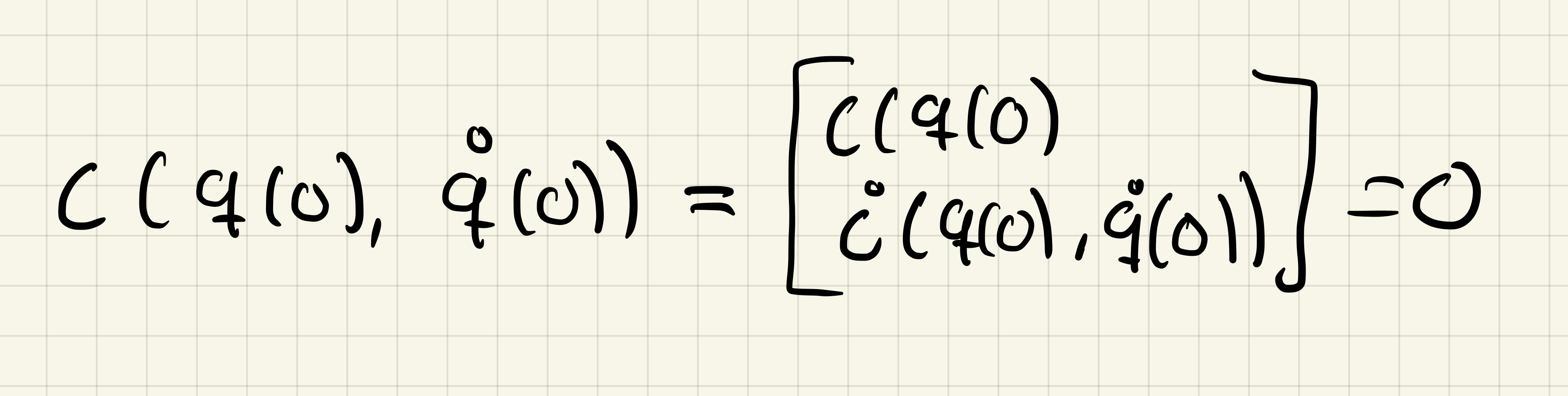Assignment 6 - Lagrange 2

In this assignment we will study the modeling of complex mechanical systems using the Constrained Lagrange equations. Since the calculations of the partial derivatives of the Lagrangian can be involved, we will once more outsource this task by using the Matlab Symbolic Math Toolbox™

Problem 1 (Hovering Mass)

Principal Rotation Matrix

Rotation around an axis. Positive angle with the clock (Positive if vector with clock, and frame against clock).

---

$$\begin{array}{rl}{\mathbf{R}}_z(\alpha )& =\left[\begin{array}{ccc}\cos \alpha & -\sin \alpha & 0\\ \sin \alpha & \cos \alpha & 0\\ 0& 0& 1\end{array}\right]\\ {\mathbf{R}}_{\mathbf{y}}(\theta )& =\left[\begin{array}{ccc}\cos \theta & 0& \sin \theta \\ 0& 1& 0\\ -\sin \theta & 0& \cos \theta \end{array}\right]\\ {\mathbf{R}}_x(\varphi )& =\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \varphi & -\sin \varphi \\ 0& \sin \varphi & \cos \varphi \end{array}\right]\end{array}$$

Link to original

a)

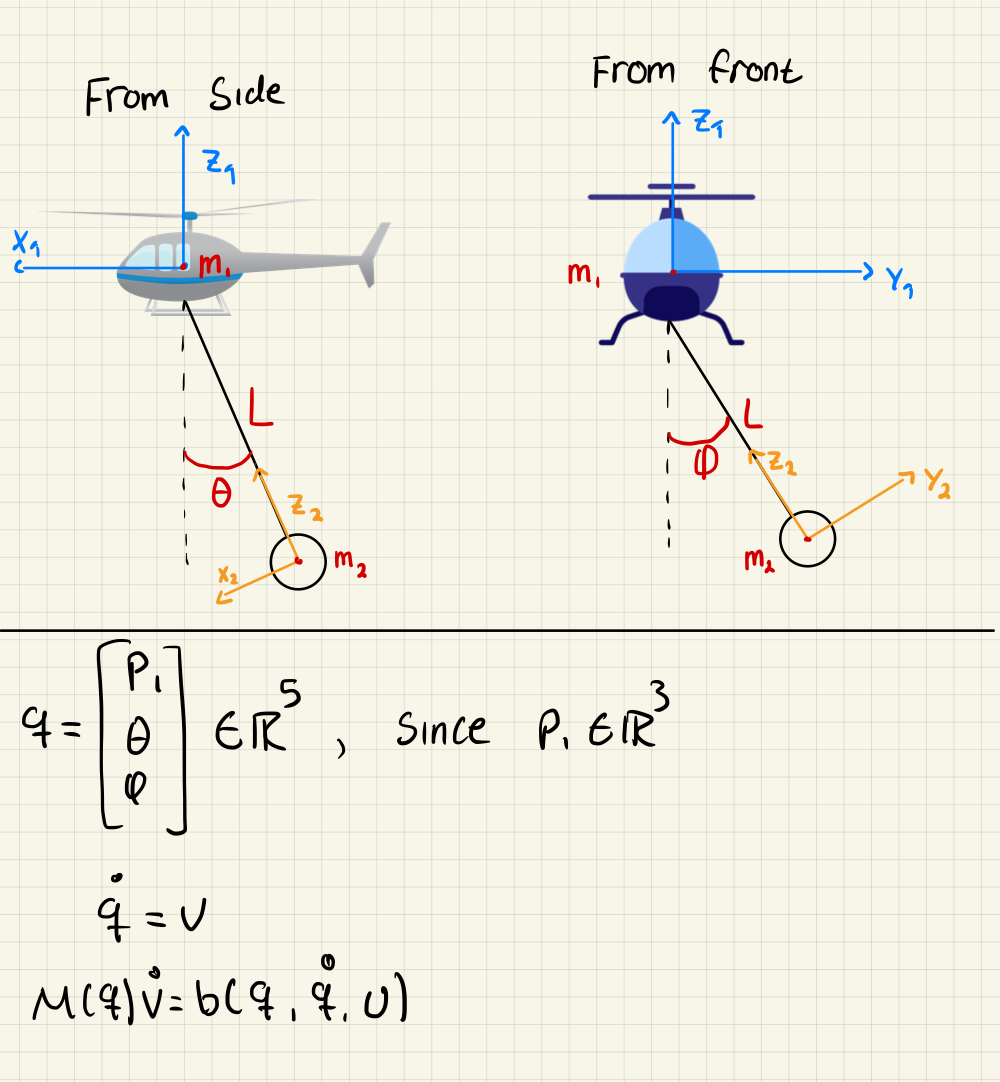
The following Matlab script implements this

clear all
clc
 
% Parameters
syms m1 m2 L g real
%Force
u = sym('u', [3,1]);
 
% Position of point mass 1
pm1 = sym('p1', [3,1]);
dpm1 = sym ('dp1', [3,1]);
ddpm1 = sym('d2p1', [3,1]);
% Angles for point mass 2
a = sym('a', [2,1]); % a(1) is theta, a(2) is phi
da = sym('da', [2,1]);
dda = sym('d2a', [2,1]);
% Generalized coordinates
q = [pm1; a];
dq = [dpm1; da];
ddq = [ddpm1; dda];
 
% Position of point mass 2
pm2 = pm1 + L* [-sin(a(1))*cos(a(2));
                sin(a(2)); 
                -cos(a(1))*cos(a(2))];
% Velocity of point mass 2
dpm2 = jacobian(pm2, q)*dq;
% Generalized forces
Q = [u; 0; 0];
% Kinetic energy
T = 1/2*m1*dpm1.'*dpm1 + 1/2*m2*dpm2.'*dpm2;
T = simplify(T);
%Potential energy
V = g*(m1*pm1(3)+m2*pm2(3));
%Lagrangian
Lagr = T-V;
 
% Derivatives of the Lagrangian
Lagr_q = simplify(jacobian(Lagr,q)).';
Lagr_qdq = simplify(jacobian(Lagr_q.',dq));
Lagr_dq = simplify(jacobian(Lagr,dq)).';
Lagr_dqdq = simplify(jacobian(Lagr_dq.', dq)); %W
 
% Matrices for problem 1
M = Lagr_dqdq
b = Q + simplify(Lagr_q - Lagr_qdq*dq) 

b)

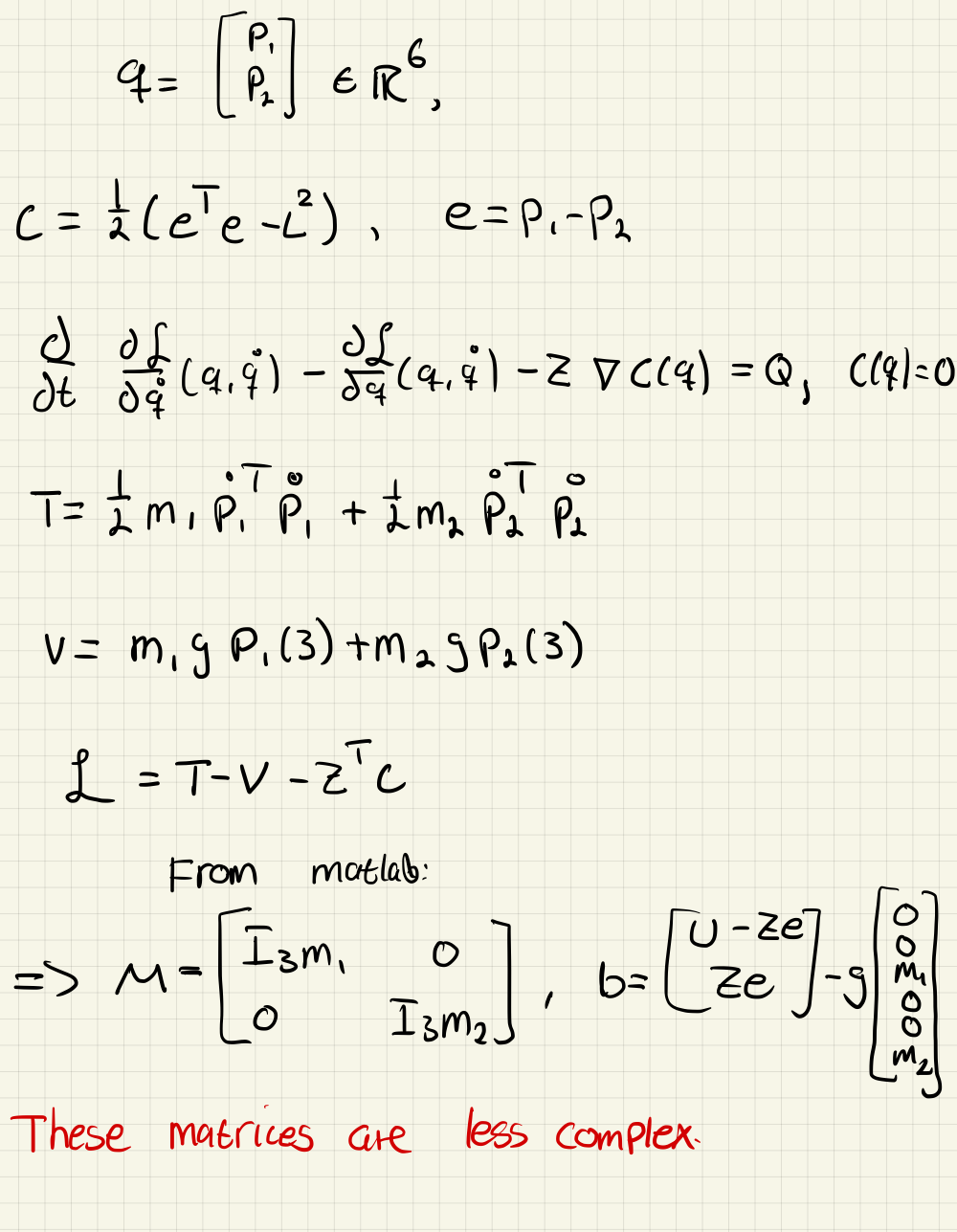
Problem 2 ($\Delta$-robot)

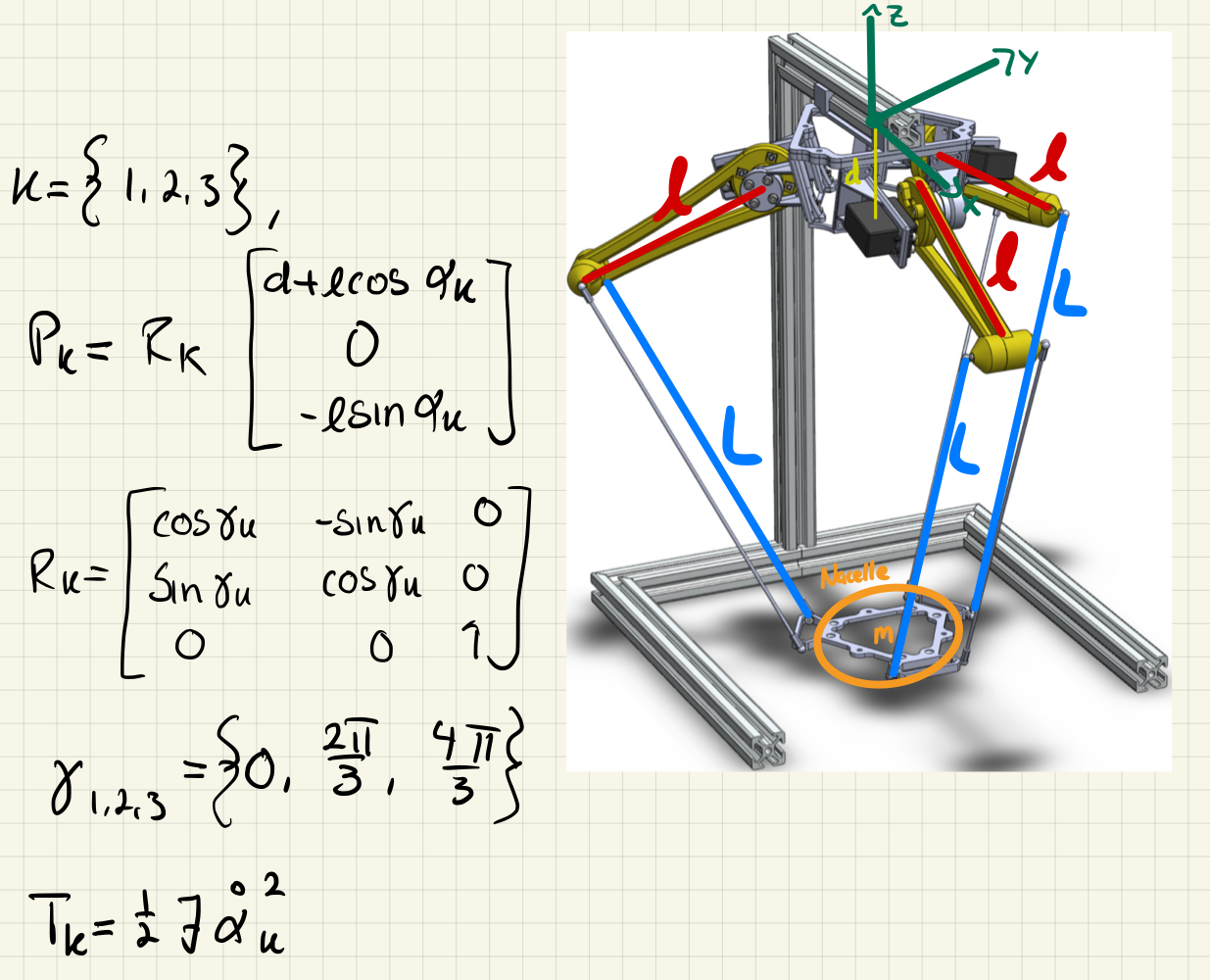
a)

b)

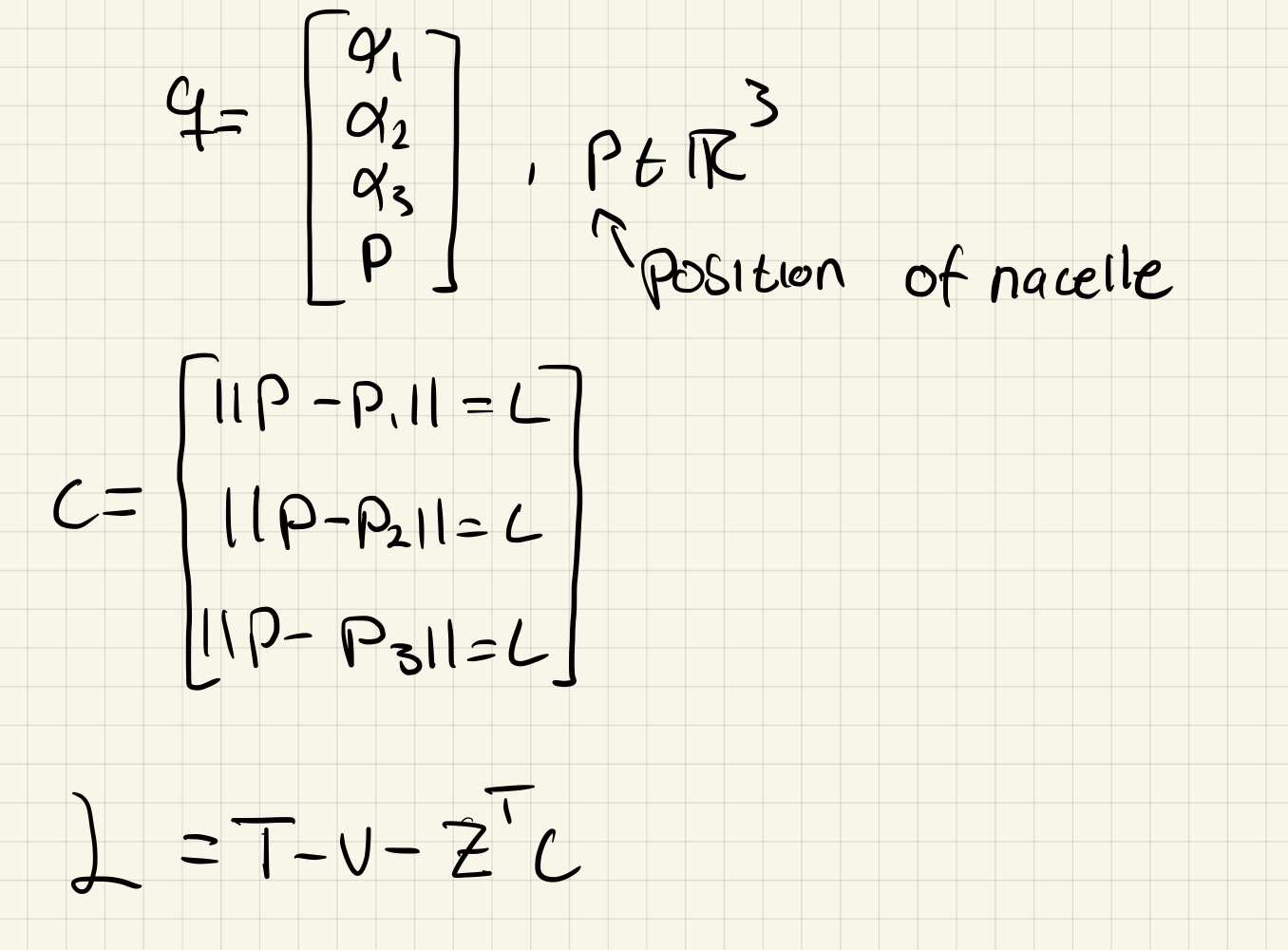
c)

The differential index of a DAE is the number of times $\frac{d}{dt}$ must be applied in order to turn the DAE into an ODE.

Link to original

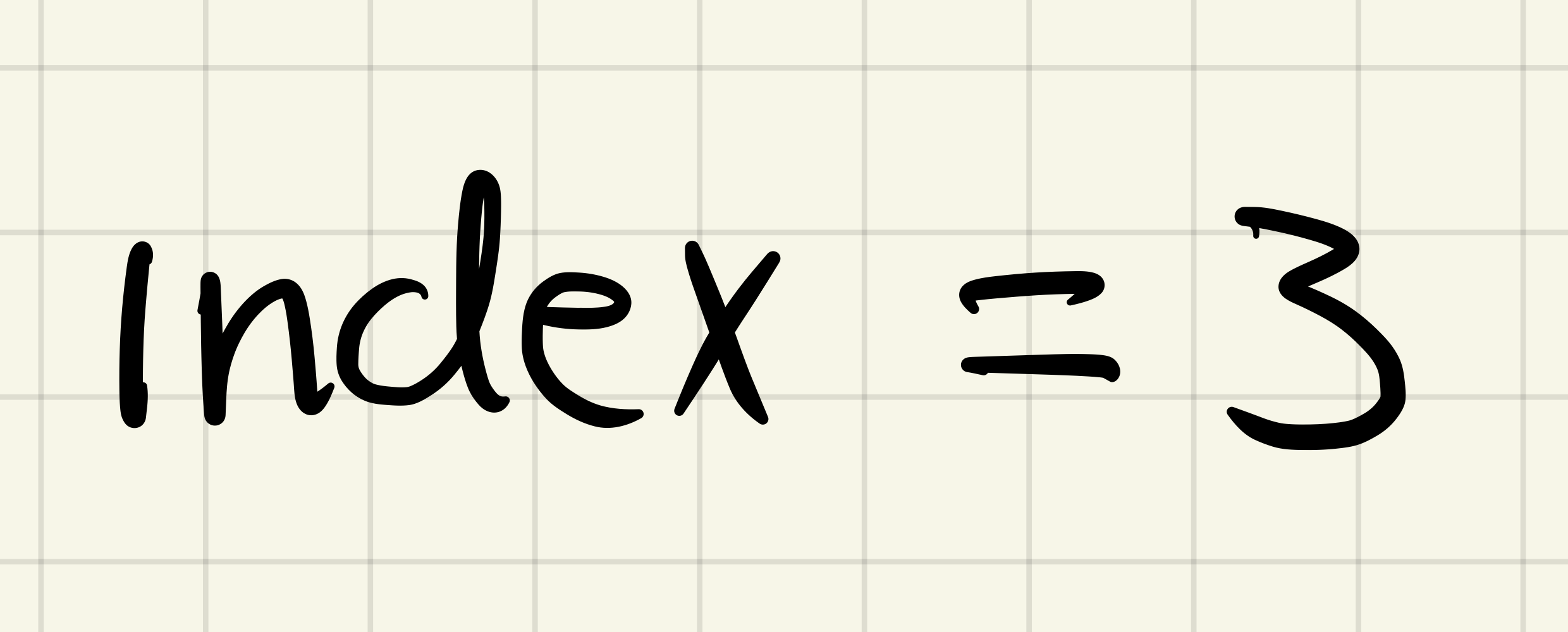
d)

Consistency Condition

Assume a hard problem (Differential Index > 1)

$$\begin{array}{rl}\dot{x}& =f(x,z)\\ 0& =c(x,z)\to 0=c^{(n-1)}(x,z)\text{ such that }\frac{\partial c^{(n-1)}}{\partial z}\text{ is full rank}\end{array}$$

How to ensure that $c^{(n-1)}=0$ implies that $c=0$?

• Need to impose

$$\begin{array}{rl}c(t=0)& =0\\ \dot{c}(t=0)& =0\\ \ddot{c}(t=0)& =0\\ ⋮& \\ c^{(n-2)}(t=0)& =0\\ c^{(n-1)}(t)& =0\end{array}$$Link to original