Recursion tree

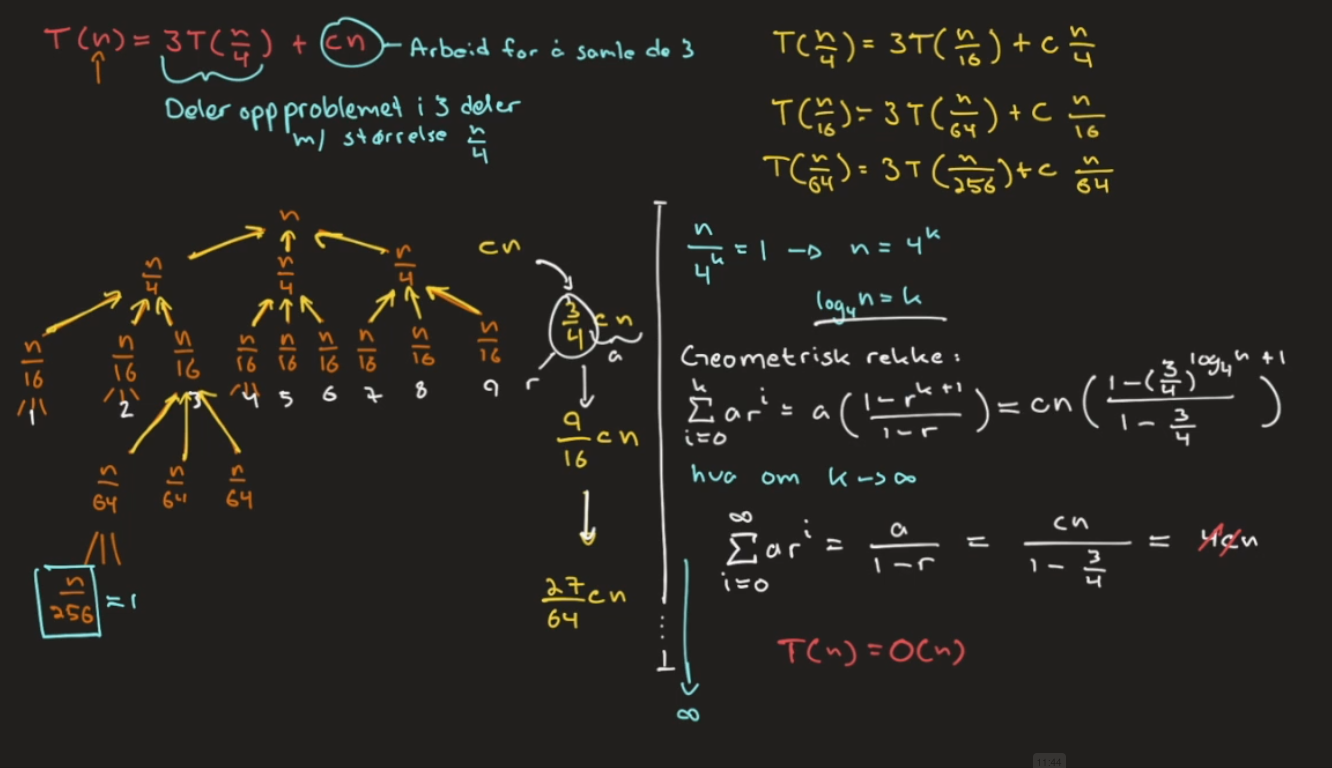
Where the Substitution Method would prove that the solution to a recurrence is correct, a recursion tree would help us coming up with a good guess for the runtime page=144

Main Idea

Given a Recurrence Equations, $T(n)=a\ast T(n/b)+f(n)$.

• a is the number of branches
• b is how large those branches are
• f(n) is the merge cost (for example $cn$)
• The height of the tree, k, is given by $\frac{n}{b^k}=1$ The height of the tree, k, is the same as $lg(n)$.
  We divide (branch out) and conquer (sort the arrays) before we merge them again.

If we encounter recurrences with square roots, we do this trick: Given $T(n)=2T(\sqrt{n})+lg(n)$ Trick $n=2^m$ Then $T(2^m)=2T(\sqrt{2^m})+lg(2^m)=2T(2^{m/2})+m$ $T(2^m)=S(m)=2S(m/2)+m$ We can then use Master-theorem on S(M) → $S(m)=O(m\ast lg(m))=T(2^m)$ → $T(n)=O(lg(n)\ast lg(lg(n)))$, where $m=lg(n)$

Examples

$T(n)=3\ast T(n/4)+cn$

$T(n)=T(n/10)+T(n/5)+T(n/3)+n^3$

We want the height of the tree in this task, and $n^3$ only tells us about the cost of merging