Assignment 1 - Introduction to modsim

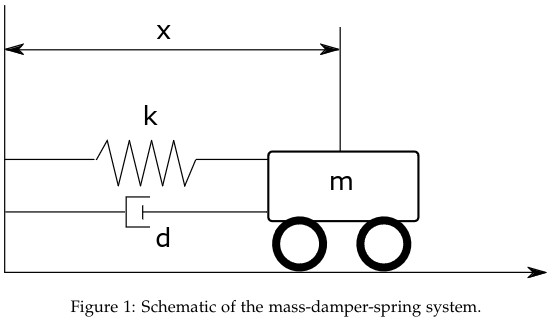
Problem 1 (Mass-damper-spring system)

a) From Hooke’s law we know that the spring force is $F_s=-kx$. We also know that the damping force is given by $F_d=-dv=-d\dot{x}$. We therefore get.

$$\begin{array}{rl}\sum F=-kx-d\dot{x}& =ma=m\ddot{x}\\ \ddot{x}+\frac{d}{m}\dot{x}+\frac{k}{m}x& =0\end{array}$$

b) We set $x_2={\dot{x}}_1$ and $x_1=x$. We therefore get the following State Space Representation model.

$$\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\end{array}\right]=\left[\begin{array}{cc}0& 1\\ -\frac{k}{m}& -\frac{d}{m}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$$

c)

import numpy as np
import matplotlib.pyplot as plt
 
# Constants
m = 1
k = 1
d = 0.7
init_x1 = 1 # initial position
init_x2 = 0 # initial velocity
 
 
# Simulation parameters
dt = 0.01
t_0 = 0
t_f = 60
num_steps = int((t_f - t_0) / dt)
 
 
def euler_forward_integration_method(x_1, x_2, dt):
	time_steps = [t_0]
	x_1_values = [init_x1]
	x_2_values = [init_x2]
	j=0
	while time_steps[j] <= t_f:
		# Calculate x_2
		dot_x_2 = -k/m * x_1 - d/m * x_2
		x_2 = x_2 + dot_x_2 * dt
		# Calculate x_1
		dot_x_1 = x_2
		x_1 = x_1 + dot_x_1 * dt
		  
		
		# Append values to lists
		time_steps.append(time_steps[j] + dt)
		x_1_values.append(x_1)
		x_2_values.append(x_2)
		
		j += 1
	
	return time_steps, x_1_values, x_2_values
 
  
 
def main():
	# Euler Forward Integration Method
	time_steps, x_1_values, x_2_values = euler_forward_integration_method(init_x1, init_x2, dt)
	
	# Plot
	plt.plot(time_steps, x_1_values)
	plt.plot(time_steps, x_2_values)
	plt.xlabel("Time (s)")
	plt.ylabel("Position (m)")
	plt.title("Euler Forward Integration Method")
	plt.legend(["Position", "Velocity"])
	plt.show()
 
  
 
if __name__ == "__main__":
	main()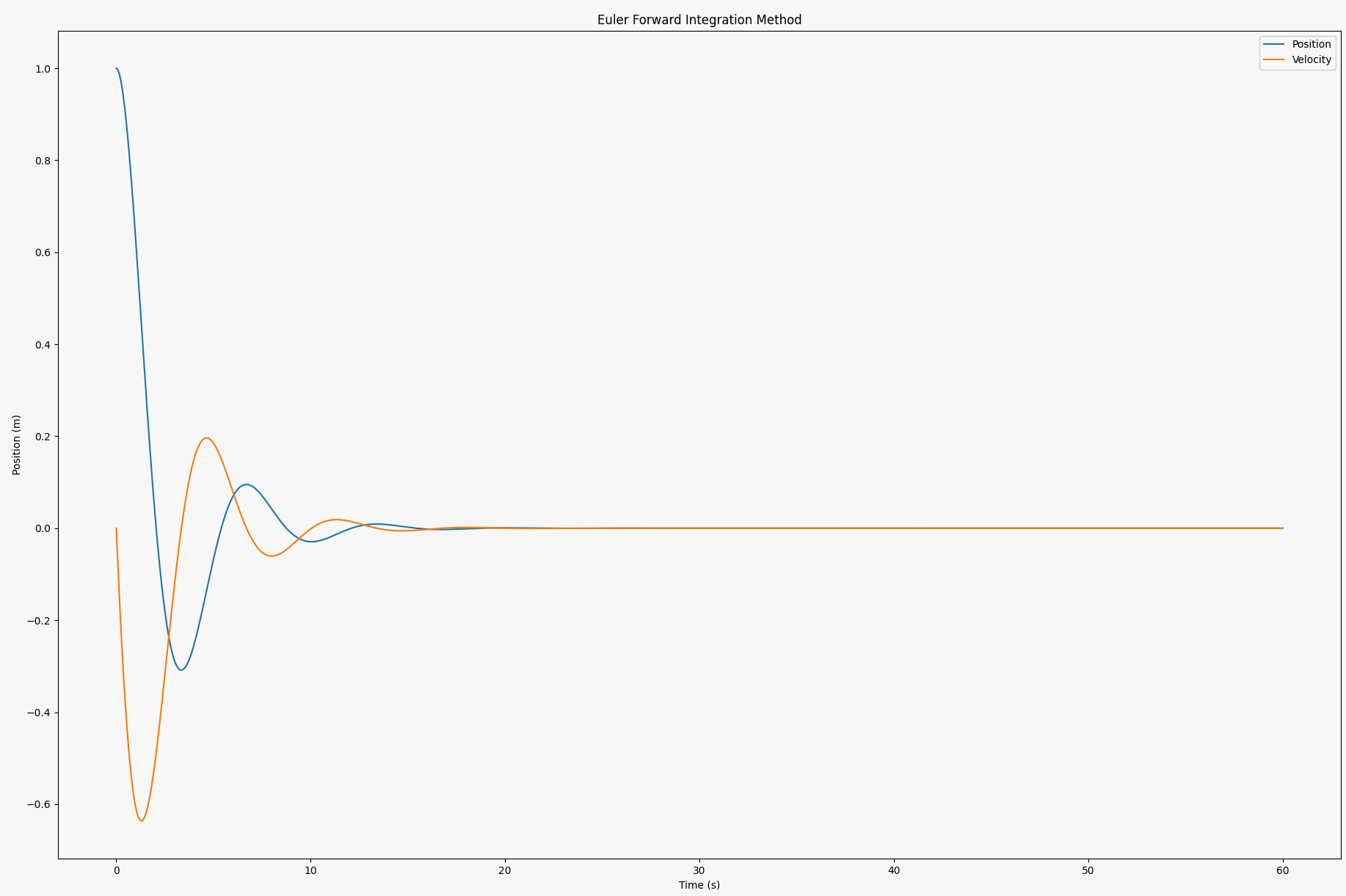

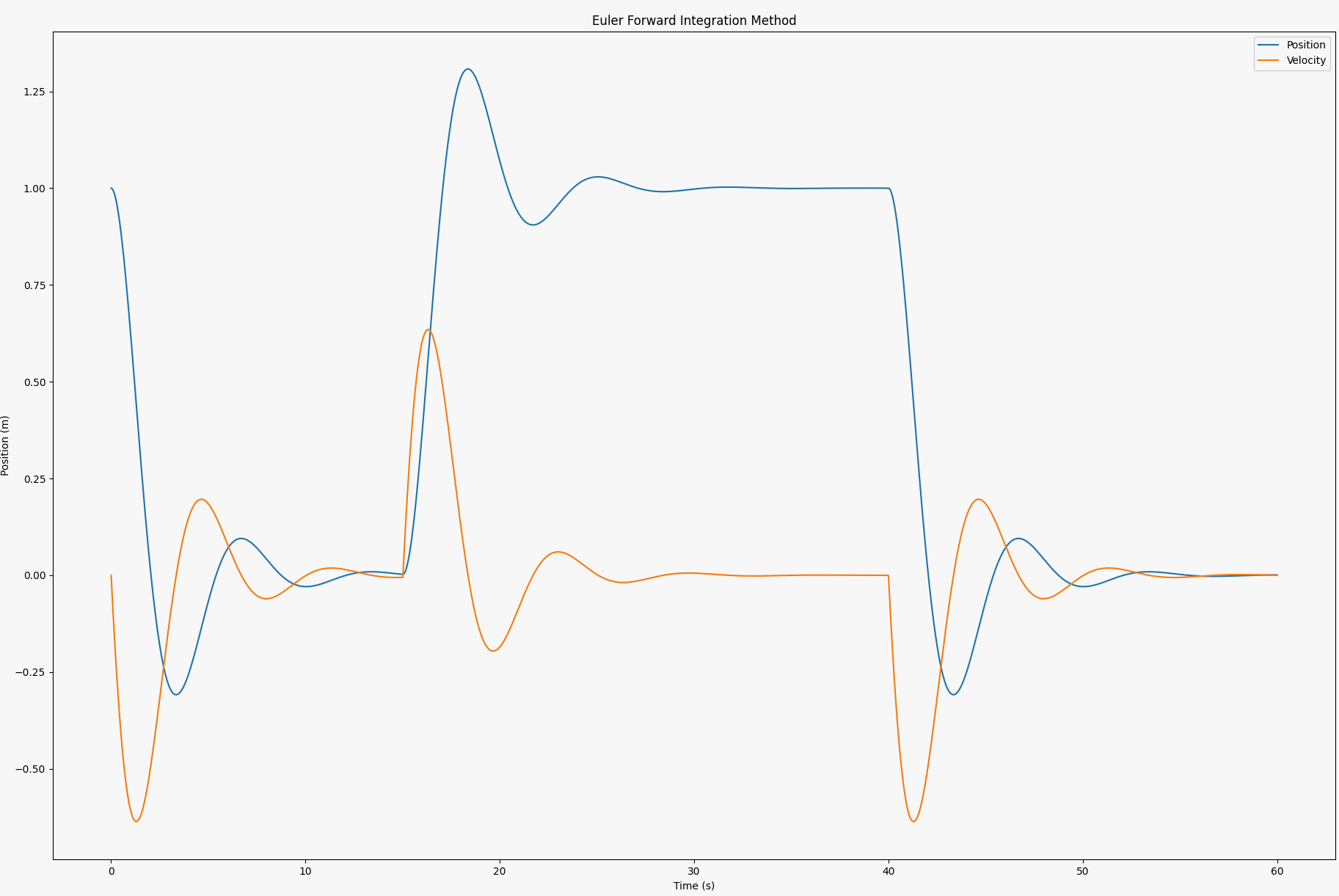
d) The expression where an outside force is acting on the wagon is given by

$$\begin{array}{rl}\sum F_x=-kx-d\dot{x}+F(t)& =m\ddot{x}\\ \ddot{x}+\frac{d}{m}\dot{x}+\frac{k}{m}x& =\frac{F(t)}{m}\end{array}$$

By adding the following code block in the while loop, we can find the inhomogeneous solution.

#...Previous code
 
# Calculate F
if time_steps[j] >= 15 and time_steps[j] <= 40:
	F = 1
else:
	F = 0
 
# Calculate x_2
dot_x_2 = -k/m * x_1 - d/m * x_2 + F/m
 
#...Rest of code

Which gives this response