Exercise 6 - MPC and LQR

Problem 1 (30%) Finite-Horizon LQR

Newtons Second Law of Motion

$F=ma$

a)

We set $m=1$, $F=u$, $x_1$ is the position, and $x_2={\dot{x}}_1$ is the velocity. We therefore get

$$\begin{array}{rl}{\dot{x}}_1& =x_2\\ {\dot{x}}_2& =\frac{F}{m}=\frac{u}{m}=u\end{array}$$

We can write this on continuous time state space form

$$\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\end{array}\right]=\underset{A_c}{\underbrace{\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]}}\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]+\underset{b_c}{\underbrace{\left[\begin{array}{c}0\\ 1\end{array}\right]}}u$$

b)

We use a sampling interval of $T=0.5$, and we can rewrite the system as a discrete system. We therefore get

$$\begin{array}{rl}A& =e^{A_{c}T}\\ A& =\sum _{k=0}^{\infty }\frac{1}{k!}{T}^k{A}_c^k\end{array}$$

Since $A_c^k=0,\forall k\ge 2$, we can write $A$ as

$$\begin{array}{rl}A& =I+T{A}_c\\ A& =\left[\begin{array}{cc}1& T\\ 0& 1\end{array}\right]\\ A& =\left[\begin{array}{cc}1& 0.5\\ 0& 1\end{array}\right]\end{array}$$

We then find $b$

$$\begin{array}{rl}b& =\left({\int }_0^T{e}^{A_c\tau }d\tau \right)b_c\\ b& =\left({\int }_0^T\left[\begin{array}{cc}1& \tau \\ 0& 1\end{array}\right]d\tau \right)\left[\begin{array}{c}0\\ 1\end{array}\right]\\ b& ={\int }_0^T\left[\begin{array}{c}\tau \\ 1\end{array}\right]d\tau \\ b& =\left[\begin{array}{c}\frac{1}{2}{\tau }^2\\ \tau \end{array}\right]{|}_{\tau =0}^{\tau =T}\\ b& =\left[\begin{array}{c}1/8\\ 1/2\end{array}\right]=\left[\begin{array}{c}0.125\\ 0.5\end{array}\right]\end{array}$$

Q.E.D

c)

The cost function for optimal control is given by

$$f(z)=\frac{1}{2}\sum _{t=0}^{N-1}\{x_{t+1}^{T}Q{x}_{t+1}+u_t^{T}R{u}_t\}$$

Where

$$Q=\left[\begin{array}{cc}2& 0\\ 0& 2\end{array}\right]\text{and}R=2$$

And $z=[x_1^T,\dots ,x_n^T,u_0^T,\dots ,u_{N-1}^T{]}^T$.

The Riccati equation for this problem is then given by

$$P_t=Q+A^T{P}_{t+1}(\mathbb{I}+b{R}^{-1}{b}^T{P}_{t+1}{)}^{-1}A,t=0,\dots ,N-1$$

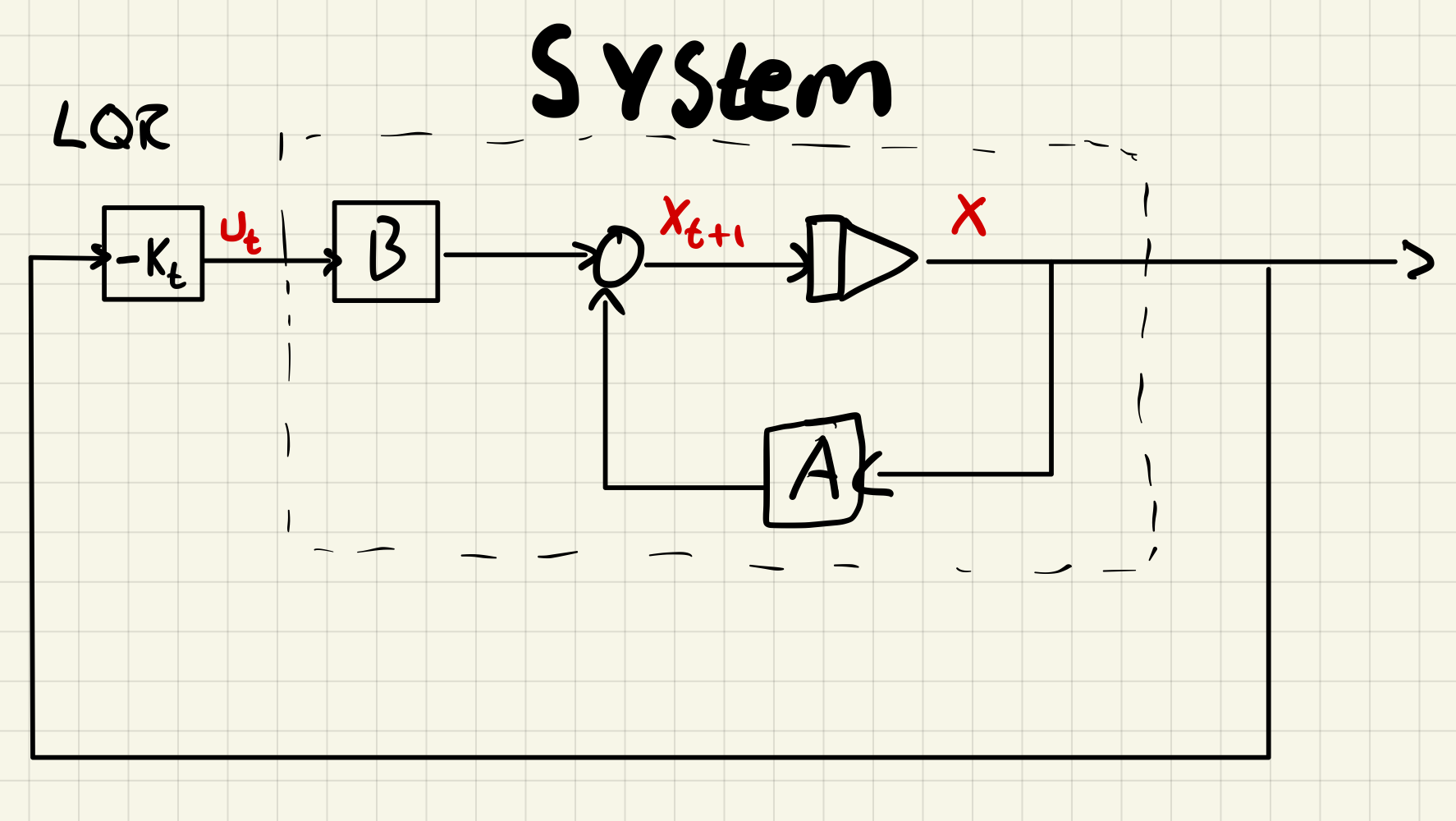
Where $P_N=Q$. We then find the feedback gain matrix, $K_t$, which is used in $u_t=-K_t{x}_t$

$$K_t=R^{-1}{b}^T{P}_{t+1}(\mathbb{I}+b{R}^{-1}{b}^T{P}_{t+1}{)}^{-1}A,t=0,\dots ,N-1$$

The system can be illustrated as

d)

We want to solve the stationary Riccati equation as $N\to \infty$. The following Matlab script (note the function dlqr) finds the optimal feedback law $u_t=-K{x}_t$.

% System matrices
A = [1  0.5;
     0  1  ];
b = [0.125;  0.5];
 
% LQR cost matrices
Q = diag([2 2]);
R = 2;
 
[~,P] = dlqr(A,b,Q/2,R/2)

Which gives the following output

P =
 
    4.0350    2.0616
    2.0616    4.1438

We then need to find $K_t$ using $P$, and find the closed-loop eigenvalues to determine the stability of the system

% Feedback gain matrix
I = eye(2);
K = (1/(R/2))*b'*P*((I+b*(1/(R/2))*b'*P)\A);
 
% Closed-loop eigenvalues
eigenvalues_closed_loop = eig(A-b*K);
abs(eigenvalues_closed_loop)

We then get the following output

ans =
 
    0.6514
    0.6514  

Since the magnitude of the eigenvalues are less than $1$, the discrete system is asymptotically stable.

e)

An infinite horizon LQ controller always yields an asymptotically stable closed-loop given that

1. $(A,B)$ witholds the Stabilizability criterion
2. ($A,D$) witholds the Detectability criterion where $Q=D^{T}D$

Problem 2 (20%) Infinite-Horizon Linear-Quadratic Control

We have the following discrete-time system

$$x_{t+1}=3x_t+2u_t,x_t,u_t\in {\mathbb{R}}^1$$

And the cost function

$$f^{\infty }(z)=\frac{1}{2}\sum _{t=0}^{\infty }\{q{x}_{t+1}^2+u_t^2\},q>0$$

a)

The Riccati equation is given by

$$P_t=Q+A^T{P}_{t+1}(\mathbb{I}+B{R}^{-1}{B}^T{P}_{t+1}{)}^{-1}A,t=0,\dots ,N-1$$

Then when it is stationary, $P_t=P_{t+1}=P$, giving

$$P=Q+A^{T}P(\mathbb{I}+B{R}^{-1}{B}^{T}P{)}^{-1}A,t=0,\dots ,N-1$$

The scalar version is

$$\begin{array}{rl}p& =q+a^{2}p\frac{1}{1+\frac{b^{2}p}{r}}\\ p& =q+\frac{a^{2}pr}{r+b^{2}p}\end{array}$$

Since $Q=2$, $R=1$, $A=3$ and $B=2$, we get

$$\begin{array}{rl}p& =2+\frac{3^{2}p}{1+2^{2}p}\\ p& =2+\frac{9p}{1+4p}\end{array}$$

Rewriting this we get

$$p^2-4p-\frac{1}{2}=0$$

Which yields the solutions $p=2\pm \frac{3}{2}\sqrt{2}$, but since $p>0$ we get that $p=2+\frac{3}{2}\sqrt{2}$.

b)

Similarly, we need to solve the scalar version of this equation

$$K=R^{-1}{B}^{T}P(\mathbb{I}+B{R}^{-1}{B}^{T}P{)}^{-1}A,t=0,\dots ,N-1$$

With $p=2+\frac{3}{2}\sqrt{2}$. This yields

$$\begin{array}{rl}k& =\frac{abp}{r+b^{2}p}\\ k& =\frac{3\cdot 2\left(2+\frac{3}{2}\sqrt{2}\right)}{1+2^2\left(2+\frac{3}{2}\sqrt{2}\right)}\\ k& =\sqrt{2}\end{array}$$

We therefore get that the optimal feedback $u_t$ is given by

$$u_t=-\sqrt{2}{x}_t$$

c)

Same answer as in e)

Transclude of Exercise-6---MPC-and-LQR#e

Problem 3 (50%) MPC and Input Blocking

The plant model is given by

$$\begin{array}{rl}{x}_{t+1}& =\underset{A}{\underbrace{\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 1\\ 0.1& -0.79& 1.78\end{array}\right]}}{x}_t+\underset{B}{\underbrace{\left[\begin{array}{c}1\\ 0\\ 0.1\end{array}\right]}}{u}_t\\ y_t& =\underset{C}{\underbrace{\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}}{x}_t\end{array}$$

We have that $x_0=[0,0,1{]}^T$, and wish to solve a finite horizon ($N<\infty$) optimal control problem with the following cost function

$$f(y_1,\dots ,y_N,u_0,\dots ,u_{N-1})=\sum _{t=0}^{N-1}\{y_{t+1}^2+r{u}_t^2\},r>0$$

Where $r=1$ (unless otherwise noted), $N=30$ and we have the following input constraint

$$-1\le u\le 1,t\in [0,N-1]$$

a)

From Exercise 5 - Open-Loop Optimal Control and MPC

Transclude of Exercise-5---Open-Loop-Optimal-Control-and-MPC#f

b)

Uses 5 iterations

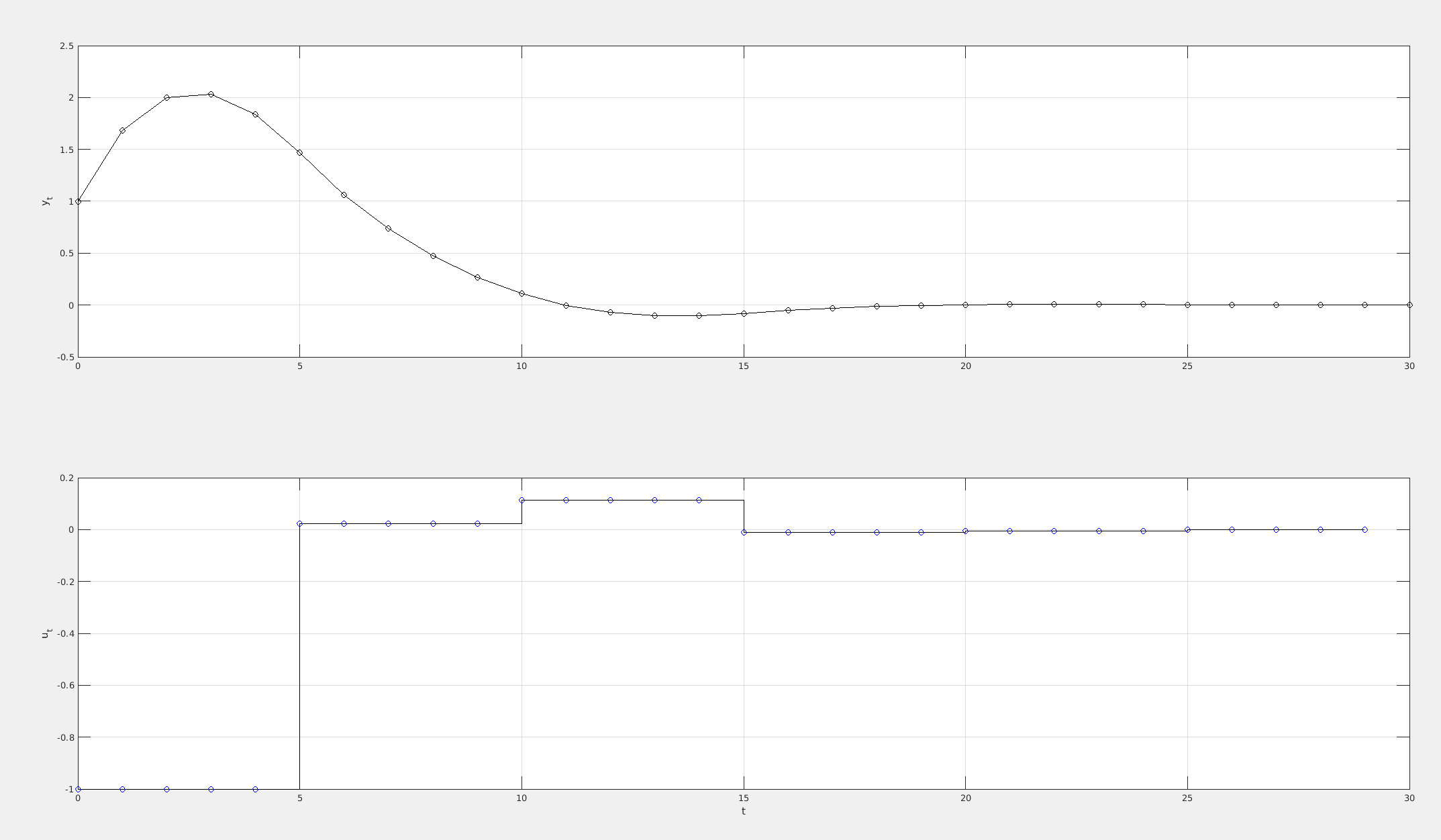
c)

No, still 5 iterations

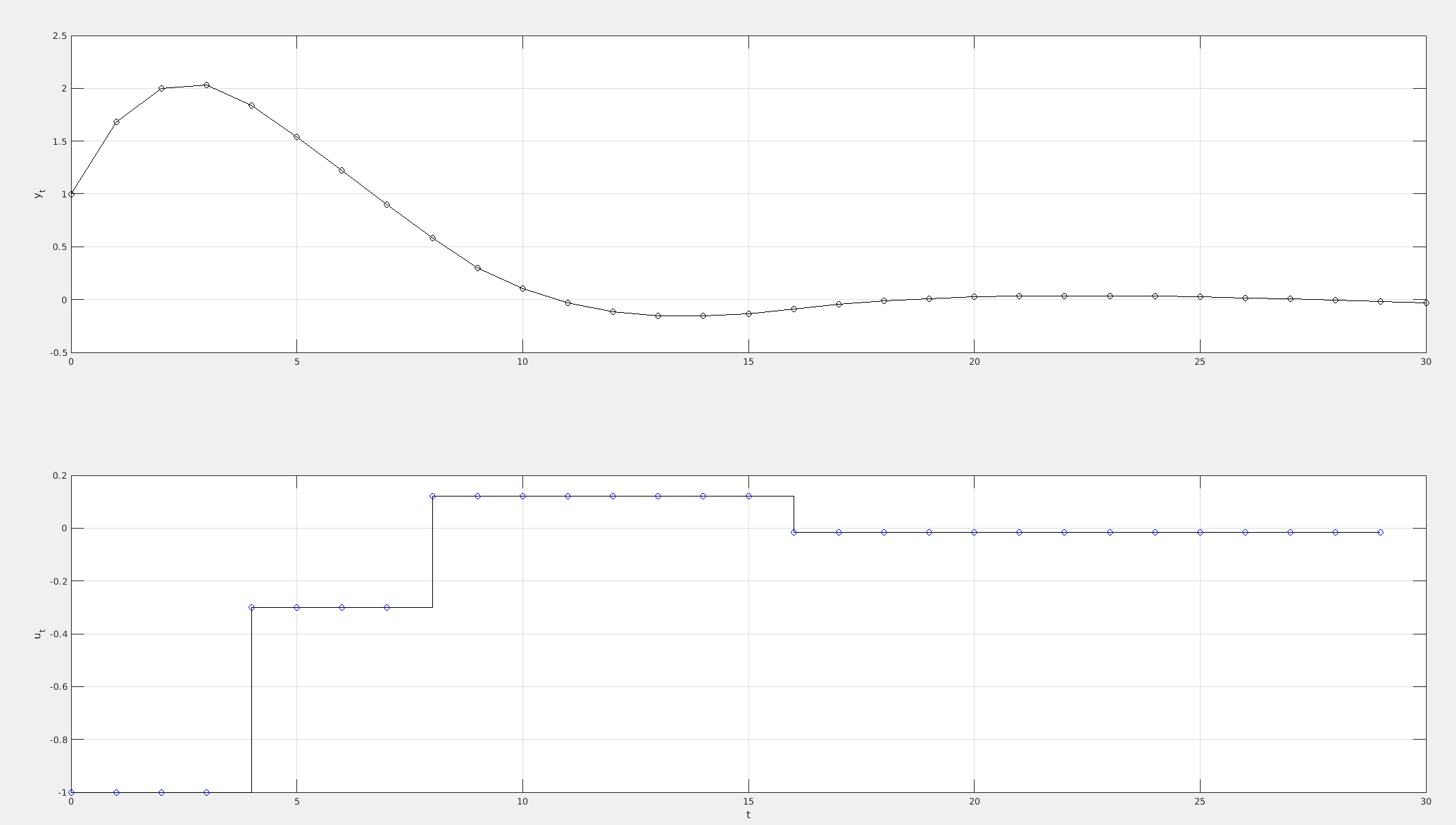
d)

Did not to the rest