Separation Principle

The separation principle tells us that the overall loop is stable if the state-feedback and observer are individually stable.

---

However, it rarely works in a practical system (why?).

Definitions

Certainty Equivalence

If the full state is not available for feedback, one can use the estimate $\hat{x}$. The estimate is generated from the output $y$, thus giving it the name output feedback.

Link to original

Output feedback controller

The feedback no longer consists of a simple constant matrix $K$, but is in fact a dynamic system of its own. This adds complexity.

Link to original

In most real words cases we don’t have access to all states.

Formulas

Given a general State Space Representation where $D=0$

Link to original

And an observer

Link to original

And $u=-K\hat{x}+K_{r}r$, where $K_r=[C(BK-A{)}^{-1}B{]}^{-1}$

This gives us the estimate update equation

$$\dot{\hat{x}}=A\hat{x}+B[-K\hat{x}+K_{r}r]+L[y-C\hat{x}]=(A-BK-LC)\hat{x}+B{K}_{r}r+Ly$$

This can be represented through the following block diagram 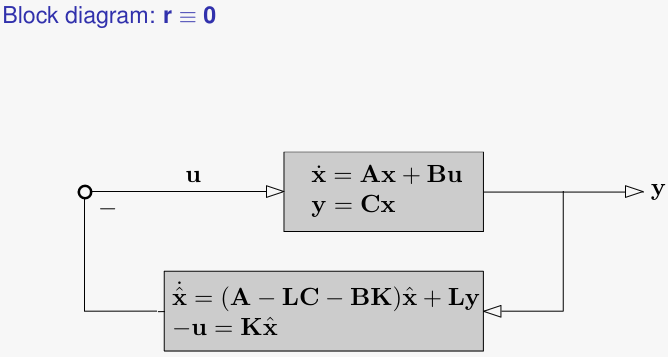And we can write the closed-loop dynamics as

$$\left[\begin{array}{c}\dot{x}\\ \dot{e}\end{array}\right]=\left[\begin{array}{cc}A-BK& BK\\ 0& A-LC\end{array}\right]\left[\begin{array}{c}x\\ e\end{array}\right]$$

IMPORTANT TO NOTE: Since it is a triangular matrix, the eigenvalues of the system is the union of the eigenvalues of $A-BK$ and $A-LC$.