Assignment 3

Problem 1

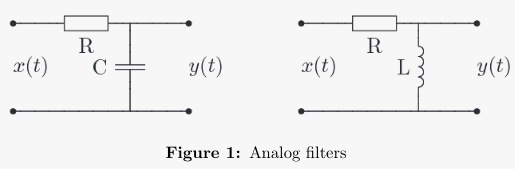
a) For the capacitor filter, we have the following equation:

$$x(t)=Ri+y(t)$$

Where $i=C\frac{dy(t)}{dt}$, which gives us:

$$x(t)=RC\frac{dy(t)}{d}+y(t)$$

And we can find the transfer function by finding $H(s)=\frac{Y(s)}{X(s)}$

x(t) = RC \frac{dy(t)}{d} + y(t) &\xrightarrow{\mathcal{L}} X(s) = RC*sY(s)+Y(s) \\ H(s) &= \frac{Y(s)}{X(s)}=\frac{1}{RCs+1} \end{align}

---

For the induction filter, we have the following equation:

$$y(t)=Ri+y(t)$$

where $y(t)=L\frac{di(t)}{dt}$, which gives us:

x(t) &= Ri + L \frac{di(t)}{dt} \\ \dot{x}(t) &= R \dot{i}(t) + \dot{y}(t) \\ \dot{x}(t) &= \frac{R}{L}y(t) + \dot{y}(t) \\ \end{align}

And we can find the transfer function by finding $H(s)=\frac{Y(s)}{X(s)}$:

\mathcal{L}[\dot{x}(t)] &= X(s) = \frac{R}{L}Y(s)+sY(s) \\ H(s) = \frac{Y(s)}{X(s)} = \frac{s}{s+\frac{R}{L}} \end{align}

b) The frequency response for the RL filter is given by:

$$H(\Omega )=H(s){|}_{s=j\omega }=\frac{j\omega }{j\omega +\frac{R}{L}}$$

And the magnitude response of the RL filter is given by:

$$|H(\Omega )|=\frac{\omega }{\sqrt{(\frac{R}{L}{)}^2+{\omega }^2}}$$

We can determine the filter characteristics by:

$$|H(0)|=0,|H(\infty )|=1$$

Which means that the RL filter is a high pass filter

---

The frequency response for the RC filter is given by:

$$H(\Omega )=H(s){|}_{s=j\omega }=\frac{1}{RCj\omega +1}$$

And the magnitude response of the RL filter is given by:

$$|H(\Omega )|=\frac{1}{\sqrt{(\omega RC{)}^2+1}}$$

We can determine the filter characteristics by:

$$|H(0)|=1,|H(\infty )|=0$$

Which means that the RC filter is a low pass filter

c) We can rewrite our expression for the RC filter and get:

$$H(s)=\frac{\frac{1}{RC}}{s+\frac{1}{RC}}$$

and since we know that ${\mathcal{L}}^{-1}\left(\frac{1}{s+a}\right)=e^{-a\ast t}u(t)$, then:

$$h(t)=\frac{1}{RC}{e}^{-1/RC\ast t}u(t)$$

which is the unit pulse response for the RC filter

---

Same logic for the RL filter

$$H(s)=\frac{s}{s+\frac{R}{L}}=1-\frac{\frac{R}{L}}{s+\frac{R}{L}}$$

which gives us:

$$h(t)=\delta (t)-\frac{R}{L}{e}^{-R/L\ast t}u(t)$$

which is the unit pulse response for the RL filter

Problem 2

Region of Convergence

If a system is causal, the ROC is defined as $|z|>|p_{max}|$, where $p_{max}$ is the pole with the largest magnitude

If a system anti-causal, the ROC is defined as $|z|<|p_{min}|$, where $p_{min}$ is the pole with the smallest magnitude

(page=163)

Link to original

a) Since the filter $H_1$ is causal, and the largest pole is $\frac{2}{3}$, the ROC and unit pulse reponse is given by: ROC: $|z|>\frac{2}{3}$

$$h_1[n]={\mathcal{Z}}^{-1}\left(\frac{1}{1-\frac{2}{3}{z}^{-1}}\right)=a^{n}u(n)$$

b) Since the filter $H_2$ is causal, and the largest pole is $1$, the ROC and unit pulse reponse is given by: ROC: $|z|>1$

h_{2}[n] &= \mathcal{Z}^{-1} \left( \frac{1}{\left( 1+\frac{1}{2}z^{-1} \right)(1-z^{-1})} \right) \\ h_{2}[n] &= \mathcal{Z}^{-1} \left( \frac{\frac{1}{3}}{1+\frac{1}{2}z^{-1}}+\frac{\frac{2}{3}}{1-z^{-1}} \right) \\ h_{2}[n] &= \left( \frac{1}{3}\left( -\frac{1}{2} \right)^n + \frac{2}{3} \right)u(n) \end{align}

Solved step 1 $\to$ 2 using WolframAlpha

c) Since the filter is anti causal, and the smallest pole is at $-\frac{3}{2}$, the ROC and unit pulse response is given by: ROC: $|z|<\frac{3}{2}$

h_{3}[n] &= \mathcal{Z}^{-1}\left( \frac{z^{-1}}{\left( 1+\frac{3}{2}z^{-1} \right)(1-3z^{-1})} \right) \\ h_{3}[n] &= \mathcal{Z}^{-1}\left( \frac{-\frac{2}{9}}{1+\frac{3}{2}z^{-1}} + + \frac{\frac{2}{9}}{1-3z^{-1}}\right) \\ h_{3}[n] &= \left( \frac{2}{9}*\left( -\frac{3}{2} \right)^n -\frac{2}{9}3^n \right)u(-n-1) \end{align}

Also used wolframalpha here.

d) A system is stable if the ROC contains the unit circle $\to$ filter $h_1[n]$ and $h_3[n]$ are stable

Problem 3

The following is important for this problem

Geometric series

Infinite geometric series

$$\sum _{n=0}^{\infty }a{r}^n=\sum _{n=1}^{\infty }a{r}^{n-1}=\frac{a}{1-r}$$

for $|r|<1$

Finite geometric series

$$\sum _{k=0}^{n-1}a{r}^k=\sum _{k=1}^{n}a{r}^{k-1}=\{\begin{array}{l}a\frac{1-r^n}{1-r},r\ne 1\\ an,r=1\end{array}$$Link to original

---

a)

H(z) &= \sum_{n=-\infty}^{\infty}h[n]z^{-n} \\ &= \sum_{n=0}^{\infty} \frac{1}{2^n}z^{-n} \\ &= \sum_{n=0}^{\infty} \left( \frac{z^{-1}}{2} \right)^n \\ &= \frac{1}{1-\frac{1}{2}z^{-1}} \end{align}

for $|z|>\frac{1}{2}$, and

X(z) &= \sum_{n=-\infty}^{\infty} x(n)z^{-n} \\ &=\sum_{n=2}^{\infty}z^{-n} \\ &=\sum_{n=0}^{\infty} z^{-n-2} \\ &=z^{-2} \sum_{n=0}^{\infty} z^{-n} \\ & = z^{-2} \frac{1}{1-z^{-1}} \end{align}

For $|z|>1$

b) We can see that

$$h[n]=\frac{1}{2^n}u(n)andx[n]=u(n-2)$$

Therefore

$$\begin{array}{rl}y[n]& =h[n]\ast x[n]\\ & =\sum _{k=-\infty }^{\infty }h[k]x[n-k]\\ & =\sum _{k=-\infty }^{\infty }\frac{1}{2^k}u(k)u(n-2-k)\\ & =\sum _{k=0}^{\infty }\frac{1}{2^k}u(n-2-k)\end{array}$$

And since our unit step response is zero for values $n-2-k<0$, then $k>n-2$. Which gives us

$$\begin{array}{rl}y[n]& =\{\begin{array}{ll}{\sum }_{k=0}^{n-2}{\left(\frac{1}{2}\right)}^k& ,n-2\ge 0\\ 0& ,n-2<0\end{array}\\ & =\{\begin{array}{ll}\frac{\left(1-{\left(\frac{1}{2}\right)}^{n-1}\right)}{1-\frac{1}{2}}=2-{\left(\frac{1}{2}\right)}^{n-2}& ,n-2\ge 0\\ 0& ,n-2<0\end{array}\\ y[n]& =(2-(\frac{1}{2}{)}^{n-2})u(n-2)\end{array}$$

c) In the z-domain, convolution is just multiplication, which gives us

Y(z) &= H(z)X(z) \\ &= \frac{1}{1-\frac{1}{2}z^{-1}} * z^{-2} \frac{1}{1-z^{-1}} \\ \end{align}

And taking the inverse Z-transform in WolframAlpha gives me:

$$\begin{array}{r}{\mathcal{Z}}^{-1}(Y(z))=y(n)=(2-(\frac{1}{2}{)}^{n-2})u(n-2)Q.E.D\end{array}$$

The math was simply time consuming to do, but with partial fractions it becomes possible to do by hand.

Problem 4

a) We Z transform and find $\frac{Y(z)}{X(z)}$:

$$\begin{array}{rl}\mathcal{Z}\to Y& =X-X{z}^{-2}-\frac{1}{4}Y{z}^{-2}\\ H(z)& =\frac{1-z^{-2}}{1+\frac{1}{4}{z}^{-2}}\end{array}$$

b) The poles are given by:

$$1+\frac{1}{4}{p}^{-2}=0\to p_1=-\frac{1}{2}j,p_2=\frac{1}{2}j$$

Zeroes are given by:

$$1-z^{-2}=0\to z_1=-1,z_2=1$$

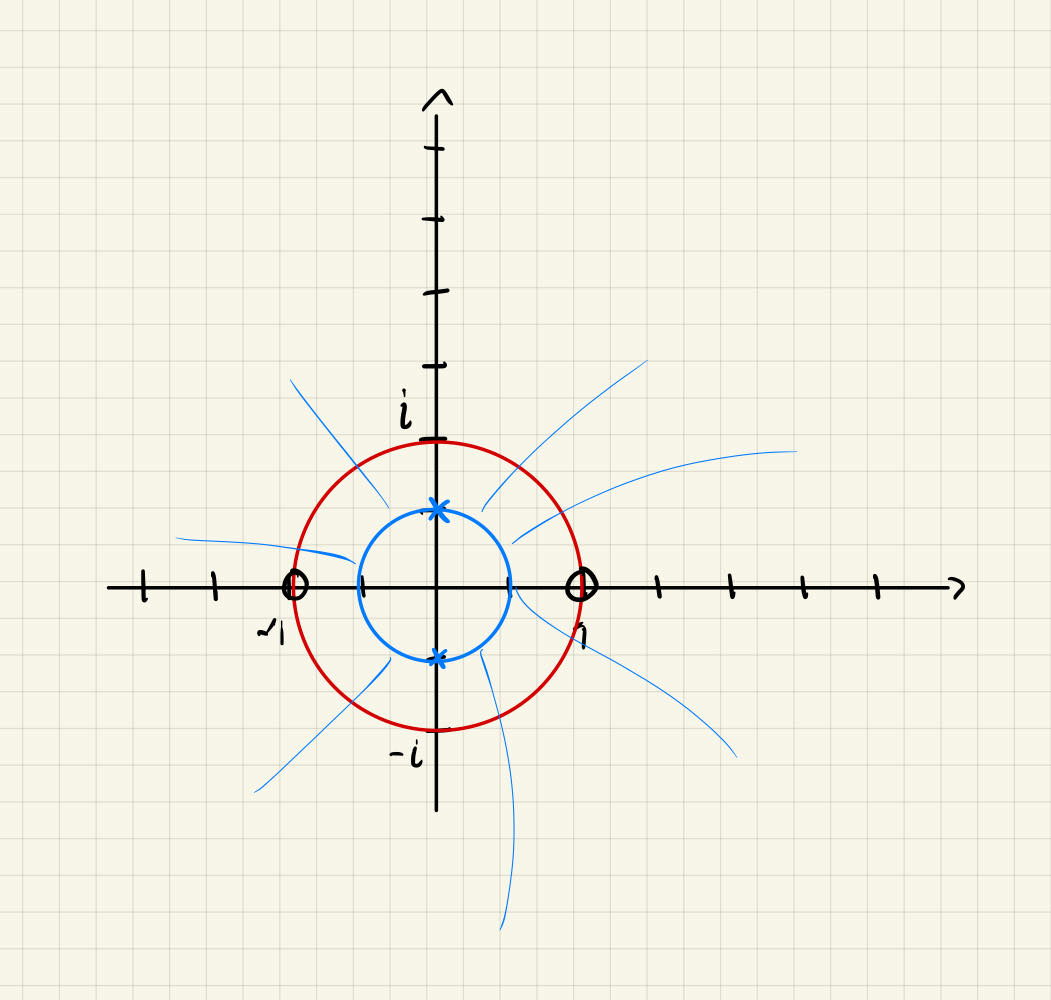
c) Since our system is causal, and the ROC contains the unit circle, the system is stable.

d) To determine the filter type we need to look at different frequencies, and evaluate the response.

For $\omega =0$: We have a zero → the amplitude is zero

for $\omega =\frac{\pi }{2}$: The distance from the zero increases, while the distance to the pole decreases → The amplitude vil reach is max at $\omega =\frac{\pi }{2}$

Same reasoning for $w=\pi$ as for $\omega =0$, and aswell as $\omega =\frac{\pi }{2}$ and $\omega =\frac{3\pi }{2}$, but this is not interesting as we only care about $0\le \omega \le \pi$

We have a bandpass filter centered around $\omega =\frac{\pi }{2}$