Assignment 4 - Newton-Euler

This assignment is about the Newton-Euler method for developing a dynamic model of a mechanical system. This topic is treated in the course book from chapter 6.13 to 7.3.

---

Problem 1 (Satellite)

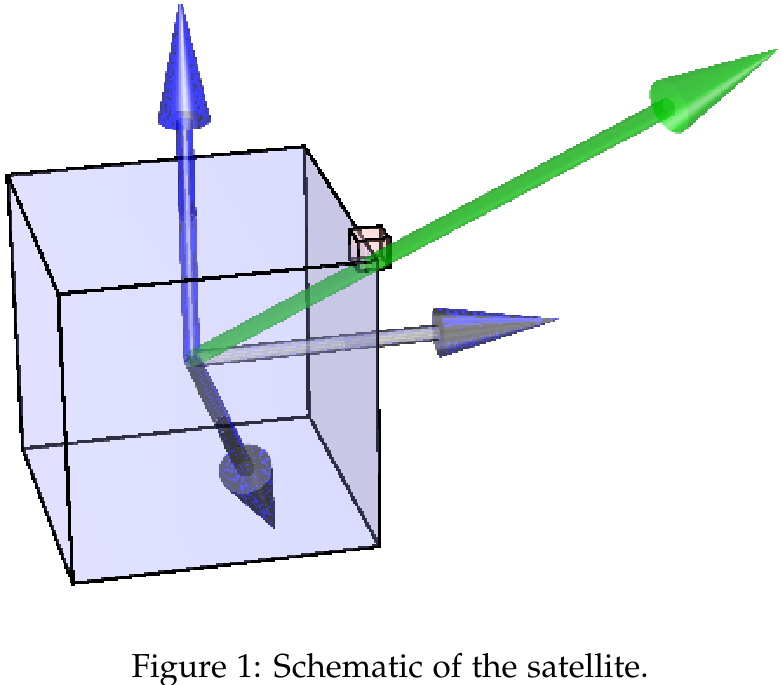
Case A:

• The satellite is a cube of uniform, unitary density, having an edge of $50$ cm
  • Unitary density → $m=l^3$ Case B:
• The satellite is the cube mentioned above, with the addition of a punctual mass of $m_0=0.1\text{ kg}$ placed at one of the cube’s corners

The force of gravity is given by

$$\vec{F}=-\frac{G{m}_{T}m}{||{\vec{r}}_c|{|}^2}\cdot \frac{{\vec{r}}_c}{||{\vec{r}}_c||}$$

The inertia matrix in the reference frame shown in the figure is

$$M_c^b=\frac{1}{6}m{l}^2{\mathbb{I}}^3$$

Which is with respect to the COM expressed in the body frame

a)

We are examining case A

We want to find ${\dot{v}}_c^i$ and ${\dot{\omega }}_{ib}^b$ by using the Newton-Euler Equations of motion.

Newton-Euler Equations of motion

Resources: page=281

---

Linear Motion (Translation)

$\sum \vec{F}=m\vec{a}$

Angular Motion (Rotation about CG)

${\dot{h}}_c=J\dot{\vec{w}}+\vec{w}\times J\vec{w}=\sum T$ Where $h=J\vec{\omega }$

Link to original

We know that the force acting on the satellite is the force of gravity, which is given. We therefore have

$$\begin{array}{rl}\sum {\vec{F}}_c^i=m{\vec{a}}_i^i& =m{\dot{\vec{v}}}_c^i\\ & \\ -\frac{G{m}_{T}m}{||{\vec{r}}_c|{|}^2}\cdot \frac{{\vec{r}}_c}{||{\vec{r}}_c||}& =m{\dot{\vec{v}}}_c^i\end{array}$$

Solution for \dot{v}_{c}^i

${\dot{\vec{v}}}_c^i={\ddot{\vec{r}}}_c^i=-\frac{G{m}_T}{||{\vec{r}}_c^i|{|}^2}\cdot \frac{{\vec{r}}_c^i}{||{\vec{r}}_c^i||}$ Where $m_T$ is the mass of earth, $G$ is the gravitational constant, and ${\vec{r}}_c^i$ is the distance from the world center to the satellites position.

We then find ${\dot{\omega }}_{ib}^b$, where the torque is zero due to there being no forces except gravity

$$\begin{array}{rlr}0& =M_c^b{\dot{\vec{\omega }}}_{b/i}^b+{\vec{\omega }}_{b/i}^b\times M_c^b{\vec{\omega }}_{b/i}^b& \\ \frac{1}{6}m{l}^2{\dot{\vec{\omega }}}_{b/i}^b& =-\left({\vec{\omega }}_{b/i}^b\times \frac{1}{6}m{l}^2{\vec{\omega }}_{b/i}^b\right)& \text{Since }\mathbb{I}v=v\end{array}$$

Solution for \dot{\vec{\omega}}_{b/i}^b

This gives us ${\dot{\vec{\omega }}}_{b/i}^b=0$ Due to ${\vec{\omega }}_{b/i}^b$ being constant. This is logical since there is nothing slowing the angular rotation (no friction etc).

b)

We are examining case B

The center of mass has now shifted due to a point mass at $m_0=0.1$ kg at one of the corners of the cube. We now need to find the new inertia matrix by using the Parallel Axis Theorem.

The new COM is given by

$$\begin{array}{rl}{\vec{r}}_{c/o}& =\frac{1}{m}\sum _k{m}_k{\vec{r}}_k\\ {\vec{r}}_{c/o}& =\frac{m_0{\vec{r}}_{m/o}+m_{cube}{\vec{r}}_{o/o}}{m_0+m_{cube}}\\ {\vec{r}}_{c/o}& =\frac{m_0{\vec{r}}_{m/o}}{m_0+m_{cube}}\end{array}$$

Then the new inertia matrix, $M_{b/o}^b$ has two contributions

$$\begin{array}{rl}{M}_{cube/0}^b& =\frac{1}{6}{m}_{cube}{l}^2\mathbb{I}\\ M_{m/0}^b& =-m_0(r_{m/0}^b{)}^{\times }(r_{m/0}^b{)}^{\times }\end{array}$$

Where the term $(r_{m/0}^b{)}^{\times }$ is the Skew-Symmetric Matrix, and

$$r_{m/c}^b=\frac{l}{2}\left[\begin{array}{c}\pm 1\\ \pm 1\\ \pm 1\end{array}\right]$$

Depending on which corner we choose. Then we can find the new inertia matrix around the new COM by using PAT

$$\begin{array}{rl}{M}_{b/o}^b& =M_{b/c}^b-(m_{cube}+m_0)(r_s^b{)}^{\times }(r_s^b{)}^{\times }\end{array}$$

Where $r_s^b=r_{o/c}^b=-r_{c/o}^b$. Solving for $M_{b/c}^b$ gives

$$M_c^b=M_{b/c}^b=\frac{1}{6}{m}_{cube}{l}^2\mathbb{I}-m_0(r_{m/0}^b{)}^{\times }(r_{m/0}^b{)}^{\times }+(m_{cube}+m_0)(r_s^b{)}^{\times }(r_s^b{)}^{\times }$$

Inserting into the following equation gives our new expression

$$\begin{array}{rl}{\dot{\vec{\omega }}}_{b/i}^b& =-(M_c^b{)}^{-1}({\vec{\omega }}_{b/i}^b\times M_c^b{\vec{\omega }}_{b/i}^b)\end{array}$$

We get the new expression for ${\dot{\vec{v}}}_c^i$, by inserting our new expression for ${\vec{r}}_c=\frac{m_0{\vec{r}}_{m/o}}{m_0+m_{cube}}$ into the following equation

$$\begin{array}{rl}{\dot{\vec{v}}}_c^i& =-\frac{G{m}_T}{||{\vec{r}}_c^i|{|}^2}\cdot \frac{{\vec{r}}_c^i}{||{\vec{r}}_c^i||}\end{array}$$

c)

Doing the following in the Satellite3DExample.m

%update the inertia matrix for the case with extra mass 
if with_added_mass
    m_added = 0.1;
    b_r_0 = l*[1;1;1]; %vector from center of the satellite to the added mass
    b_r_s = -m_added/(m_added+m)*0.25*[1;1;1]; %TODO
    % inertia matrix of satellite from cube center
    b_M_o = b_M_c - (m_added*0.25)*[0 1 -1; -1 0 1; 1 -1 0]*0.25*[0 1 -1; -1 0 1; 1 -1 0]; %TODO
    % inertia matrix of satellite from mass center
    b_M_c = b_M_o + (m_added + m)*[0 b_r_s(3) -b_r_s(2); -b_r_s(3) 0 b_r_s(1); b_r_s(2) -b_r_s(1) 0]; %TODO
end  

And the following in SatelliteDynamics.m

 Dynamics
i_v_c_dot = -G*m_T/(abs(i_r_c)).^2*i_r_c/abs(i_r_c); %TODO
b_omega_ib_dot = -inv(b_M_c)*[0 b_omega_ib(3) -b_omega_ib(2); -b_omega_ib(3) 0 b_omega_ib(1); b_omega_ib(2) -b_omega_ib(1) 0] * b_M_c*b_omega_ib; %TODO  

From the simulation (changing the boolean with_added_mass), we observe that:

Without the added mass, the angular velocity is constant, but with the added mass it changes with time.

Problem 2 (Pendulum on an Oscillator)

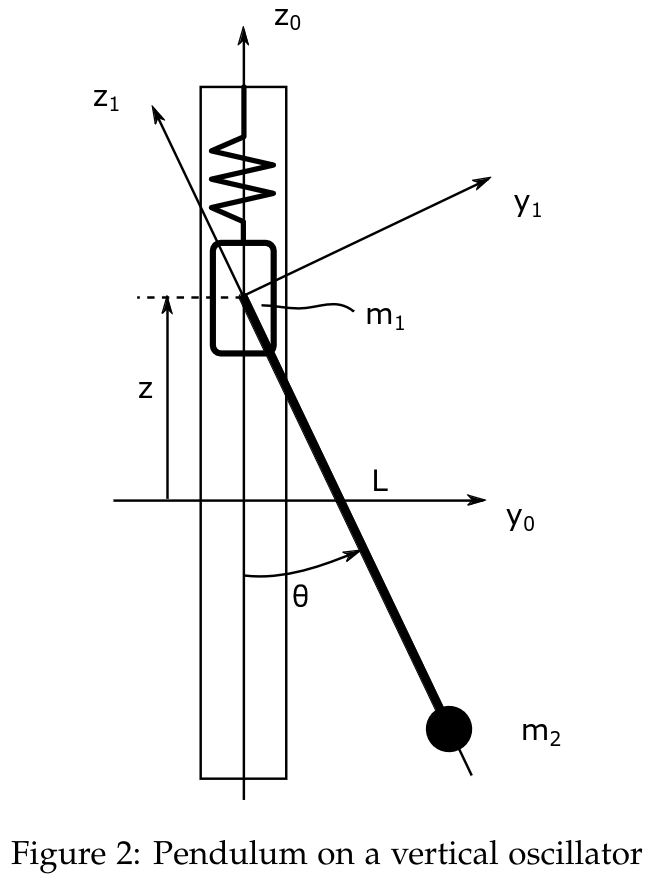
a)

The position of mass 1 can be expressed as

$${\vec{r}}_1^0=z{\vec{k}}_0$$

And the acceleration is given by

$${\vec{a}}_1={\ddot{\vec{r}}}_1=\ddot{z}{\vec{k}}_0$$

---

The position of mass 2 can be expressed as

$${\vec{r}}_{2/1}^1=-L{\vec{k}}_1$$

Or expressed in the $0$-frame as

$${\vec{r}}_2^0={\vec{r}}_1^0+R_1^0{\vec{r}}_{2/1}^1$$

Where $R_1^0=R_x(\theta )=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \theta & -\sin \theta \\ 0& \sin \theta & \cos \theta \end{array}\right]$ , and is the Principal Rotation Matrix around the $x$-axis.

$$\begin{array}{rl}{\vec{a}}_2& ={\ddot{\vec{r}}}_2\\ {\vec{a}}_2& ={\vec{a}}_1+\frac{d^2}{d{t}^2}\left(\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \theta & -\sin \theta \\ 0& \sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c}0\\ 0\\ -L\end{array}\right]\right)\\ {\vec{a}}_2& =\ddot{z}{\vec{k}}_0+\frac{d^2}{d{t}^2}\left(\left[\begin{array}{c}0\\ L\sin \theta \\ -L\cos \theta \end{array}\right]\right)\\ {\vec{a}}_2& =\ddot{z}{\vec{k}}_0+(L\ddot{\theta }\cos \theta -L{\dot{\theta }}^2\sin \theta ){\vec{j}}_0+(L\ddot{\theta }\sin \theta +L{\dot{\theta }}^2\cos \theta ){\vec{k}}_0\\ {\vec{a}}_2& =(L\ddot{\theta }\cos \theta -L{\dot{\theta }}^2\sin \theta ){\vec{j}}_0+(\ddot{z}+L\ddot{\theta }\sin \theta +L{\dot{\theta }}^2\cos \theta ){\vec{k}}_0\end{array}$$

Q.E.D

---

I realized (a bit too late) that i could’ve used the formula

$${\vec{a}}_2={\vec{a}}_1+{\vec{\alpha }}_1\times {\vec{r}}_{2/1}+{\vec{\omega }}_1\times ({\vec{\omega }}_1\times {\vec{r}}_{2/1})$$

Where ${\vec{\omega }}_1=\dot{\theta }{\vec{i}}_0$ and $\vec{\alpha }=\ddot{\theta }{\vec{i}}_0$, which would yield the same result (and being a bit easier.)

b)

From Newton-Euler Equations of motion

Newton-Euler Equations of motion

Resources: page=281

---

Linear Motion (Translation)

$\sum \vec{F}=m\vec{a}$

Angular Motion (Rotation about CG)

${\dot{h}}_c=J\dot{\vec{w}}+\vec{w}\times J\vec{w}=\sum T$ Where $h=J\vec{\omega }$

Link to original

The forces acting on mass 1 are; gravity, the spring force and the joint force.

$$\sum \vec{F}=m_1{\vec{a}}_1={\vec{F}}_{spring}+{\vec{F}}_{g1}+{\vec{F}}_{joint,1}$$

Where

$$\begin{array}{rl}{\vec{F}}_{g_1}& =-m_{1}g{\vec{k}}_0\\ {\vec{F}}_{spring}& =-kz{\vec{k}}_0\\ {\vec{F}}_{joint,1}& =-m_{2}g\cos \theta {\vec{k}}_0+m_{2}g\sin \theta {\vec{j}}_0\end{array}$$

---

The forces acting on mass 2 are; gravity and the joint force

$$\sum \vec{F}=m_2{\vec{a}}_2={\vec{F}}_{g_2}+{\vec{F}}_{joint,2}$$

Where

$$\begin{array}{rl}{\vec{F}}_{g_2}& =-m_{2}g{\vec{k}}_0\\ {\vec{F}}_{joint,2}& =-{\vec{F}}_{joint,1}=-{\vec{F}}_{joint}\end{array}$$

---

We also want the torque from mass 2. We can get this by using the formula $\vec{\tau }=\vec{r}\times \vec{F}$.

$${\vec{\tau }}_{g_2}={\vec{r}}_{2/1}\times m_2{\vec{a}}_2$$

c)

We have

$$\begin{array}{rl}& 1.{\vec{a}}_1=\left[\begin{array}{c}0\\ 0\\ \ddot{z}\end{array}\right]\\ & 2.\vec{\alpha }=\left[\begin{array}{c}\ddot{\theta }\\ 0\\ 0\end{array}\right]\\ & 3.{\vec{a}}_2={\dot{\vec{v}}}_2={\ddot{\vec{r}}}_{2/0}^0=\left[\begin{array}{c}0\\ L\ddot{\theta }\cos \theta -L{\dot{\theta }}^2\sin \theta \\ \ddot{z}+L\ddot{\theta }\sin \theta +L{\dot{\theta }}^2\cos \theta \end{array}\right]\\ & 4.m_1{\vec{a}}_1={\vec{F}}_{spring}+{\vec{F}}_{g1}+{\vec{F}}_{joint}\\ & 5.m_2{\vec{a}}_2={\vec{F}}_{g_2}-{\vec{F}}_{joint}\\ & 6.{\vec{\tau }}_{g_2}={\vec{r}}_{2/1}\times m{\vec{a}}_2\end{array}$$

Since we know that

$${\vec{F}}_{joint}=m_1\left[\begin{array}{c}0\\ 0\\ \ddot{z}\end{array}\right]+m_1\left[\begin{array}{c}0\\ 0\\ g\end{array}\right]+k\left[\begin{array}{c}0\\ 0\\ z\end{array}\right]$$

We can combine equation 5 and 3 (substituting for ${\vec{F}}_{joint}$), and get

$$\begin{array}{rl}{m}_1\ddot{z}+m_{2}L{\dot{\theta }}^2\cos \theta +m_{2}L\ddot{\theta }\sin \theta +m_2\ddot{z}+m_{2}g+m_{1}g+kz& =0\\ (m_1+m_2)\ddot{z}+m_{2}L{\dot{\theta }}^2\cos \theta +m_{2}L\ddot{\theta }\sin \theta +(m_1+m_2)g+kz& =0\end{array}$$

Lastly, combining equation 5 and 6 we get

$$L^2{m}_2\ddot{\theta }+L{m}_2\ddot{z}\sin \theta +L{m}_{2}g\sin \theta =0$$

Which are the two equations we were supposed to show.

d)

The difference is that mass 2 now has a new COM, making equation 6 different (by adding a new torque), and finding the new moment of inertia. Applying this will give the new equations.

Due to the calculations being quite comprehensive, i will not be writing these in LaTeX due to the fact that i’ve already used too many hours on this, but i will give my final result.

$$\begin{array}{rl}\frac{7}{12}{L}^2{m}_2\ddot{\theta }+\frac{L}{2}{m}_2\ddot{z}\sin \theta +\frac{L}{2}{m}_{2}g\sin \theta & =0\end{array}$$

e)

By thinking of the problem as rotation around the hinge point, we neglect the interaction of the two bodies (${\vec{F}}_{joint}$)