We use the idea of Eigenvectors and Eigenvalues, which gives us information about the internal dynamics of an LTI system.
Where is the eigenvector matrix corresponding to the eigenvalue matrix
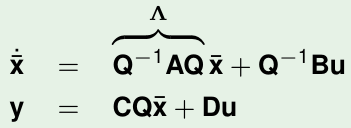
It then follows that
Where
Search
Jan 06, 2025, 1 min read
We use the idea of Eigenvectors and Eigenvalues, which gives us information about the internal dynamics of an LTI system.
Transformation Matrix - T=Q−1 → xˉ=Q−1x
Where Q is the eigenvector matrix corresponding to the eigenvalue matrix Λ
ΛQ=λ10⋮00λ20……000⋮λn=[q1q2…qn]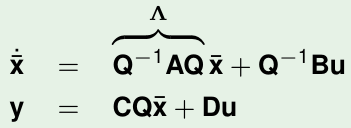
It then follows that
G(s)=Cˉ(sI−Λ)−1B^+DˉWhere
(sI−Λ)−1=s−λ110⋮00s−λ21⋮0……⋱000⋮s−λn1