Helicopter Lab Day 2

Optimal Control of Pitch/Travel without Feedback

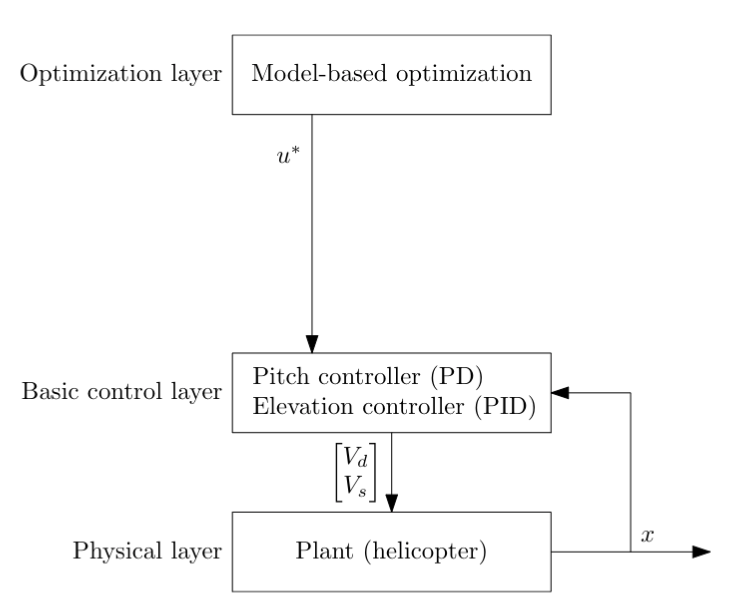
Preparations

1) State Space Formulation

State Space Representation Task We want to write the model on continuous time state space form

$$\dot{x}=A_{c}x+B_{c}u$$

Where $x={\left[\begin{array}{cccc}\lambda & r& p& \dot{p}\end{array}\right]}^T$, and $u=p_c$.

We know the following:

$$\begin{array}{rl}\ddot{p}& =K_1{V}_d\\ \dot{r}& =-K_{2}p\\ \dot{\lambda }& =r\end{array}$$

---

Solution

$$A_c=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& -K_2& 0\\ 0& 0& 0& 1\\ 0& 0& -K_1{K}_{pp}& -K_1{K}_{pd}\end{array}\right],B_c=\left[\begin{array}{c}0\\ 0\\ 0\\ K_1{K}_{pp}\end{array}\right]$$

2) Model Discretization

Task Discretize the model using the forward Euler method, and write it on the discrete time state space form

$$x_{k+1}=A{x}_k+B{u}_k$$

---

Solution Forward Euler method gives us

$$\dot{x}=\frac{x_{k+1}-x_k}{\Delta t}=A_c{x}_k+B_c{u}_k$$

Rewriting this

$$x_{k+1}=(\mathbb{I}+\Delta t{A}_c)x_k+\Delta t{B}_c{u}_k$$

Where $A=\mathbb{I}+\Delta t{A}_c$ and $B=\Delta t{B}_c$

$$A=\left[\begin{array}{cccc}1& \Delta t& 0& 0\\ 0& 1& -\Delta t{K}_2& 0\\ 0& 0& 1& \Delta t\\ 0& 0& -\Delta t{K}_1{K}_{pp}& 1-\Delta t{K}_1{K}_{pd}\end{array}\right],B=\left[\begin{array}{c}0\\ 0\\ 0\\ \Delta t{K}_1{K}_{pp}\end{array}\right]$$

3) Calculating the Optimal Path

Values:

$$\begin{array}{rlr}{\lambda }_0& =\pi & \\ {\lambda }_f& =0& \\ |p_k|& \le \frac{60\pi }{360},& \text{(aka 30 degrees)}\end{array}$$

Task Find optimal trajectory for moving from $x_0=[{\lambda }_0,0,0,0{]}^T$ to $x_f=[{\lambda }_f,0,0,0{]}^T$, when we assume that the elevation angle is constant.

Solution Why do we need this constraint?

• Large deviations from the point of linearization might lead to poor performance. Therefore (due to safety) we limit it to $30$ degrees.

Is it necessary to also implement this constraints on the pitch reference angle $p_c$?

• This is what we’ve done.

Minimizing the cost function

$$\varphi =\sum _{i=0}^{N-1}({\lambda }_{i+1}-{\lambda }_f{)}^2+q{p}_{ci}^2,q\ge 0$$

We want to express this as

$$f(z)=\sum _{t=0}^{N-1}\frac{1}{2}{x}_{t+1}^{T}Q{x}_{t+1}+\frac{1}{2}{u}_t^{T}R{u}_t$$ $$\underset{z\in R^n}{\min }f(z)=\frac{1}{2}{z}^{T}Gzs.t{A}_{eq}z=b_{eq}$$

Finding $Q$: We therefore get

$$\begin{array}{rl}({\lambda }_{i+1}-{\lambda }_f{)}^2& =\frac{1}{2}{x}_{t+1}^{T}Q{x}_{t+1}\\ ({\lambda }_{i+1}-0{)}^2& =\frac{1}{2}\left[\begin{array}{cccc}{\lambda }_{i+1}& r_{i+1}& p_{i+1}& {\dot{p}}_{i+1}\end{array}\right]\left[\begin{array}{cccc}{q}_{11}& q_{12}& q_{13}& q_{14}\\ q_{21}& q_{22}& q_{23}& q_{24}\\ q_{31}& q_{32}& q_{33}& q_{34}\\ q_{41}& q_{42}& q_{43}& q_{44}\end{array}\right]\left[\begin{array}{c}{\lambda }_{i+1}\\ r_{i+1}\\ p_{i+1}\\ {\dot{p}}_{i+1}\end{array}\right]\end{array}$$

Meaning that $q_{11}=2$, and the rest is $0$.

$$Q=\left[\begin{array}{cccc}2& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]$$

Same reasoning for finding $R$:

$$\begin{array}{rl}\frac{1}{2}{u}_i^{T}R{u}_i& =q{p}_{ci}^2\\ \frac{1}{2}{u}_i^{T}R{u}_i& =q{u}_i^2\end{array}$$

Thus giving us $R=2q$

$$\left[\begin{array}{cccccccc}\mathbb{I}& & & & -B& & & \\ -A& \mathbb{I}& & & & \ddots & & \\ & \ddots & \ddots & & & & \ddots & \\ & & -A& \mathbb{I}& & & & -B\end{array}\right]$$

3.1) For the daring

4) Adding Zeroes to the Input Vector

This is done to let the helicopter stabilize at $e=0$.

5) Elevation offset

The elevation offset is about 30 degrees. When we start the program, it thinks its current position $\vec{0}$, which is what we can offset.

6) Reasonable Trajectory

The trajectory seems reasonable considering its an open control loop.

In the Lab

See Github for Matlab implementation.

Test plan

Row vs data

1. Time
2. Travel
3. Travel rate
4. Pitch
5. Pitch rate
6. Elevation
7. Elevation rate
8. Pitch reference
9. Elevation reference
10. V_d
11. V_s 13-17. x_star (row 13-17)

For the Report

The motors are uneven, therefore $-10$ degrees on pitch makes it more stable

• If the helicopter is completely still at the start, the optimization layer works better than if its moving when the controller starts.