Discrete Time Kalman Filter

Kalman Filter in Continuous Time is not really doable in a realistic system. We therefore use the discrete time Kalman filter.

---

Quite similar to Exact Discretization. $\bar{A}$, $\bar{B}$ are the same, while $\bar{w}={\int }_0^T{e}^{A\alpha }Gw((k+1)T-\alpha )d\alpha$. Disturbance covariance - ${\int }_0^T{e}^{A\alpha }G{Q}_w{G}^T{e}^{A^T\alpha }d\alpha$ Noise covariance - ${\bar{R}}_v=\frac{R_v}{T}$

Discrete Time Kalman Gain Matrix Discrete Time Covariance Matrix of the Estimation Error

How it works

1. ComputeDiscrete Time Kalman Gain Matrix, $L[k]$
2. Update estimate with measurement, $\hat{x}[k]$
3. Update error covariance matrix, $P[k]$
4. Project ahead, aka find ${\hat{x}}^{-}[k+1]$ and $P^{-}[k+1]$
5. Repeat

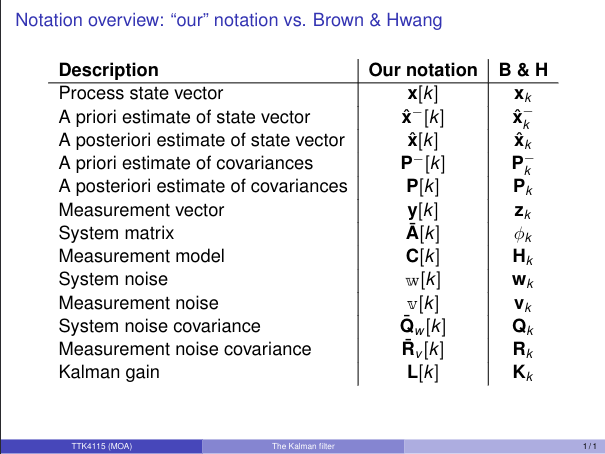
Notation

We calculate the posteriori estimate based on the priori estimate. The posteriori estimate is therefore presumed better than the priori estimate.

Discrete Observer

The estimate is done in two phases, A priori estimate, ${\hat{x}}^{-}[k]$, and an improved posteriori estimate, $\hat{x}[k]$.

$$\begin{array}{rl}{\hat{x}}^{-}[k]& =\bar{A}\hat{x}[k-1]+\bar{B}u[k-1]\\ \hat{x}[k]& ={\hat{x}}^{-}[k]+L[k](y[k]-C{\hat{x}}^{-}[k])\end{array}$$