Johnsons algoritme

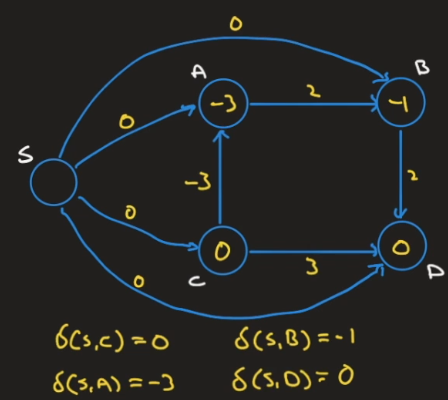
Gitt en vektet rettet graf, gir den oss en matrise som forteller oss hva korteste vei fra en node til en annen er.

---

Pseudokode og kjøretid

Kjøretid: Med min-heap - $O(VElgv)$ Med fibonacci heap - $O(V^{2}lgV+VE)$

Generelt kan vi si at kjøretiden er med en vanlig min-heap som prioritetskø i Dijkstras algoritme blir $O(VE+V^{2}lgV)$. Vi bruker denne algoritmen fremfor Floyd-Warshalls algoritme når $E\approx V$ og vi kan neglisjere $VE$ og får dermed kjøretid $O(VElgV)=O(V^{2}lgV)$ . For kompakte grafer $E\approx V^2$ vil kjøretiden bli nærmere $O(V^3)$.

Virkemåte

Baserer seg på Dijkstras algoritme, og kjører den på alle noder. Forskjellen er at denne derimot funker med negative kantvekter. Dette kan f.eks gjøres ved å gjøre alle kantene positive:

• $\cancel{\text{ce}Leggep\mathring{a}enkonstantp\mathring{a}allevektene,ogfjernekonstanteneetterp\mathring{a}.}$
  • Funker dårlig!
• Bruke en Teleskopsum
  • Kantvektene er nå definert ved $\hat{w}(u,v)=w(u,v)+h(u)-h(v)$ der $h(u)$ er verdien til node $u$, og $h(v)$ er verdien til node $v$.

Ved å bruke en teleskop sum blir denne grafen 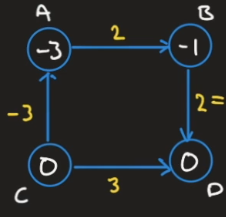Til denne 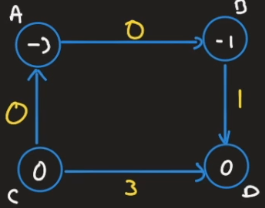Som vi kan bruke Dijkstras algoritme på. Til slutt finner vi $w(u,v)$ fra $\hat{w}(u,v)$ som er den korteste avstanden fra alle til alle.

Hvordan finne $h(\cdot )$

Trekantulikheten Den korteste veien fra $i$ til $j$ er mindre enn eller lik den korteste veien fra $i$ til $k$ pluss vekten av kanten fra $k$ til $j$.

$$\begin{array}{rl}\delta (i,j)& \le \delta (i,k)+w(k,j)\\ 0& \le w(k,j)+h(k)-h(j)=\hat{w}(k,j)\end{array}$$

---

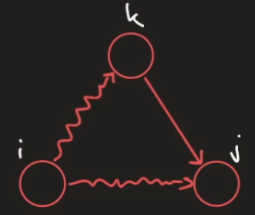
Ved å bruke dette prinsippet kan vi koble med en ekstern node, $S$, med vekter lik $0$, og kjøre Bellman-Ford. Verdien nodene får er verdien vi får i $h(\cdot )$.