Exercise 3 - LP, QP, and KKT Conditions

Lecture 4&5 - Linear Programming (LP) Quadratic Programming Problem on Standard Form KKT (Karush–Kuhn–Tucker) Conditions

Problem 1 (35%) LP and KKT Conditions (Exam August 2000)

Consider the following LP in standard form

Link to original

Where $c\in {\mathbb{R}}^n$ and $b\in {\mathcal{R}}^m$. And the KKT (Karush–Kuhn–Tucker) Conditions are given by

Link to original

a) Newton Direction

The Newton Direction is given by

Link to original

Meaning that since the Hessian is zero, the Newton Direction is not defined (dividing by zero).

b) Convex Objective Function

For a optimization problem to be convex the following must hold

Criterions

1. The objective function is a Convex Objective Function
2. The equality constraint functions $c_i(\cdot ),i\in \mathcal{E}$ are linear, and
3. The inequality constraint functions $c_i(\cdot ),i\in \mathcal{I}$, are Concave

Link to original

Finding if the objective function is convex The definition of a convex objective function is given by

Link to original

Where in our case, $f(x)=c^{T}x$.

$$\begin{array}{rl}& \alpha f(x)+(1-\alpha )f(y)\\ & =\alpha c^{T}x+(1-\alpha )c^{T}y\\ & =c^T(\alpha x+(1-\alpha )y)\\ & =f(\alpha x+(1-\alpha )y)\end{array}$$

Meaning that the objective function is convex (and actually also concave).

Since the equality and inequality constraint are linear, they are (by the same logic) both convex and concave. The problem stated in the top of the document is therefore a convex optimization problem.

c) The Dual LP Problem

From Exercise 2 - LP and KKT Conditions

e)

Using the first KKT condition

$$1.c=A^T{\lambda }^{\ast }+s^{\ast }$$

The equality constraint at $x=x^{\ast }$

$$2.A{x}^{\ast }=b$$

And the last condition

$$3.s^{\ast T}{x}^{\ast }=0$$

---

From equation 1

c^Tx^* &= (A^T\lambda^*+s^*)^Tx^* \\ &=\lambda^{*T}Ax^*+s ^{*T}x^* \\ &=\lambda^{*T}b+0 \\ &=b^T\lambda^*, \;\;\; \text{Q.E.D} \end{align}

The last line is legal since it will be the same scalar operations

Link to original

d) The Dual LP Problem

The optimal solutions of the objective functions have the same values.

e) Basic Feasible Point (BFP)

Basic Feasible Point (BFP)

page=384

---

A vector $x$ is a basic feasible point if

• $x$ is Feasible
• There exists a subset $\mathcal{B}$ of the index set $\{1,2,\dots ,n\}$ such that
  • $\mathcal{B}$ contains exactly $m$ indices
  • $i\notin \mathcal{B}\to x_i=0$ (that is, the bound $x_i\ge 0$ can be inactive only if $i\in \mathcal{B}$).
  • the $m\times m$ matrix $B$ is defined by $B=[A_i{]}_{i\in \mathcal{B}}$, and is nonsingular, and $A_i$ is the $i$‘th column of $A$.

$\mathcal{B}(x)$ is called a basis for the LP, and the indices not in $\mathcal{B}(x)$ are called $\mathcal{N}(x)$.

Link to original

f) LICQ

From the LICQ we have that

Given the point $x$ and the active set $\mathcal{A}(x)$, we say that the linear independence constraint qualification (LICQ) holds if the set of active constraint gradients $\{\nabla c_i(x),i\in \mathcal{A}(x)\}$ is linearly independent.

Link to original

We find

$${\nabla }_{x}Ax-b=A^T$$

Meaning that if $A$ has full row rank, all of the columns in the gradient are linearly independent, thus satisfying the LICQ.

Problem 2 (40%) LP

We need to put the problem on the following form

Link to original

a) Slack Variable

We set $x_1=A$ and $x_2=B$ (in $1000$ kg). We want to maximize

$$\underset{x\in {\mathbb{R}}^n}{\max }\frac{3}{2}{x}_1+x_2$$

Aka minimizing

$$\underset{x\in {\mathbb{R}}^n}{\min }-\left(\frac{3}{2}{x}_1+x_2\right)$$

Assuming that we will not have a negative price, we have $x_1,x_2\ge 0$. We also have the constraints

$$\begin{array}{rl}8& \ge 2x_1+1x_2\\ 15& \ge x_1+3x_2\end{array}$$

We want to have an equality constraint, and we therefore add a Slack Variable, giving us

$$\begin{array}{rl}A& =\left[\begin{array}{cccc}2& 1& 1& 0\\ 1& 3& 0& 1\end{array}\right]\\ c^T& =\left[\begin{array}{cc}-\frac{3}{2}& -1\end{array}\right]\\ b& =\left[\begin{array}{c}8\\ 15\end{array}\right]\end{array}$$

b)

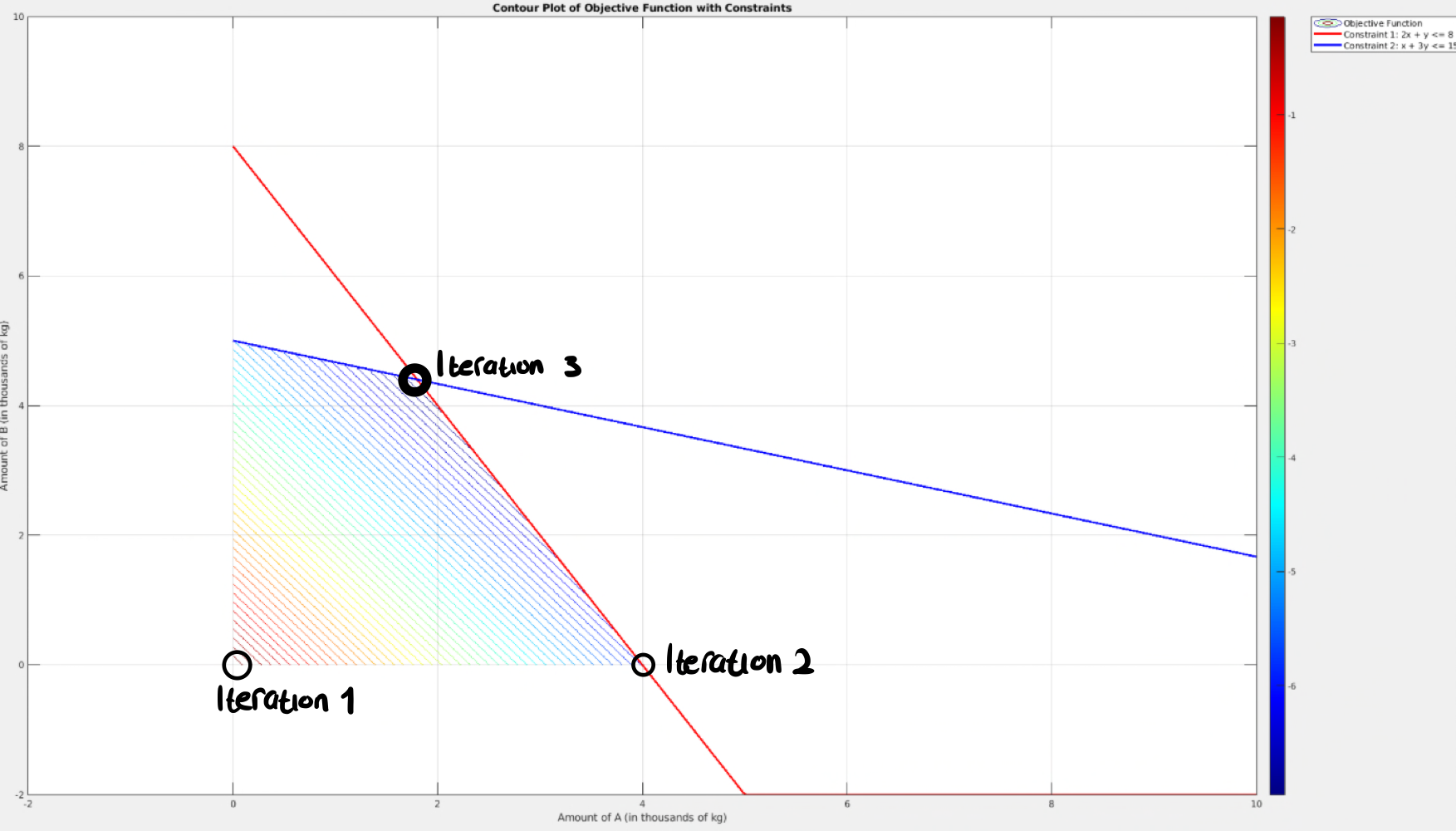
c)

As seen in the figure from b), we see that the solution is in the intersection between the constraints. The non-negative constraint is not active in iteration 3.

d)

done in b)

e)

According to the theory in Ch. 13.3 (Simplex Method), the algorithm output is expected.

Problem 3 (25%) QP and KKT Conditions (Exam May 2000)

A general QP can be formulated as

Link to original

a) Active Set

The active set is given by

Link to original

Which gives

$$\mathcal{A}(x)=\mathcal{E}\cup \{i\in \mathcal{I}|a_i^T{x}^{\ast }=b_i\}$$

b) KKT (Karush–Kuhn–Tucker) Conditions

Link to original

The Lagrangian is given by

$$\mathcal{L}(x,\lambda )=\frac{1}{2}{x}^{T}Gx+x^{T}c-\sum _{i\in \mathcal{E}\cup \mathcal{I}}{\lambda }_i(a_i^{T}x-b_i)$$

Finding the Gradient of the Lagrangian gives

$${\nabla }_x\mathcal{L}(x^{\ast },{\lambda }^{\ast })=G{x}^{\ast }+c-\sum _{i\in \mathcal{A}(x^{\ast })}{\lambda }_i^{\ast }{a}_i$$

From the complementary condition we know that the multiplier is zero if the constraint is not active at the solution.

We know that all the constraints $i$ in the active set $a_i^T{x}^{\ast }=b_i$ must hold at $x=x^{\ast }$.

From the dual feasibility criterion we know that the ineq. constraint $i$ that are not active at the soltuion $a_i^T{x}^{\ast }\ge b_i$ must hold, and that these multipliers must be greater than zero. We can therefore write the KKT conditions as

$$\begin{array}{rlr}G{x}^{\ast }+c-\sum _{i\in \mathcal{A}(x^{\ast })}{\lambda }_i^{\ast }{a}_i& =0& \text{Stationary}\\ a_i^T{x}^{\ast }& =b_i,i\in \mathcal{A}(x)& \text{Primal Feasibility}\\ a_i^T{x}^{\ast }& \ge b_i,i\in \mathcal{I}\text{textbackslash}\mathcal{A}(x^{\ast })& \text{Primal Feasibility}\\ {\lambda }_i^{\ast }& \ge 0,i\in \mathcal{I}\cap \mathcal{A}(x^{\ast })& \text{Dual Feasibility}\end{array}$$

---