The transfer function does not contain any information about the unobservable and uncontrollable parts of the system. The transfer function is by definition a relation between input and output. Realizations of transfer functions can therefore only produce the controllable and observable subsystem. WE CAN’T MAKE WHAT WE CANT SEE
We need to consider the unobservable and uncontrollable subsystems also; are they stable?
We can transform a system to decomposed form show that it has an uncontrollable/unobservable state
Motivation
Reduce the size of the system with respect to the input/output characteristics. A simplification with more theoretical gain rather than real word gain.
Example with an uncontrollable system
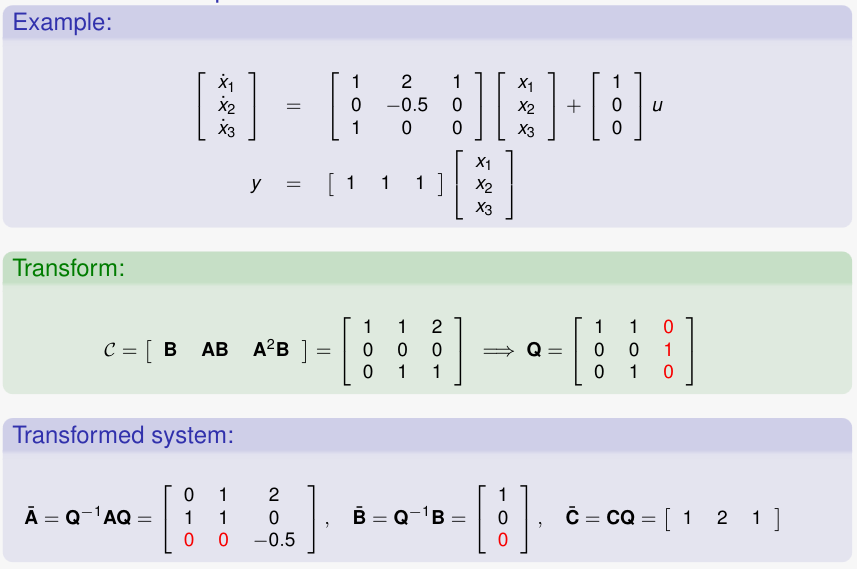 Since the controllability matrix has only two linearly independent vectors, we choose the third one in a way so that the matrix is reversible. The third state remains uncontrollable after the transformation.
Since the controllability matrix has only two linearly independent vectors, we choose the third one in a way so that the matrix is reversible. The third state remains uncontrollable after the transformation.
Example with an unobservable system
Generally:
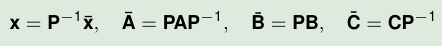 Reason:
Reason:

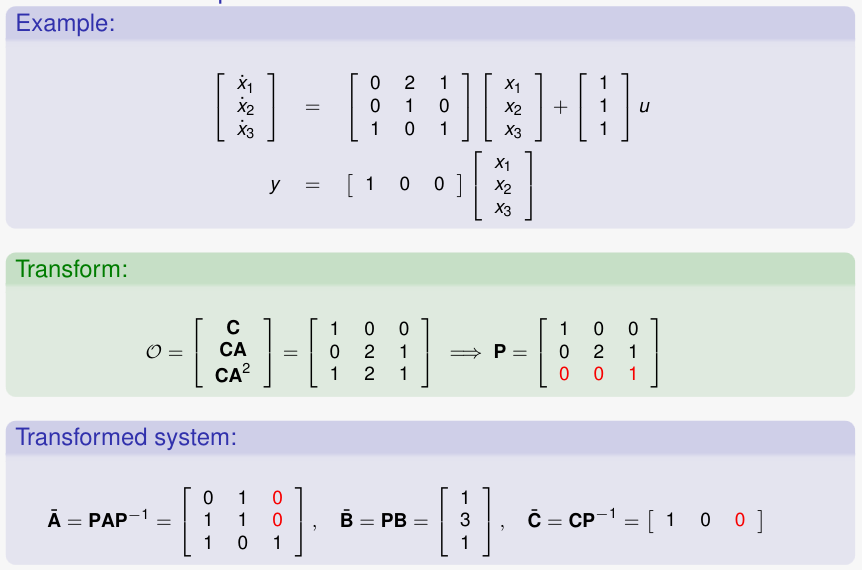
Where we fill out such that it becomes invertible.