Problem 1
Given the following equation for the system
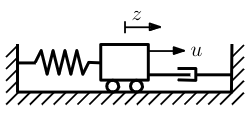
a) We can rewrite the system on State Space Representation form, where
Gives us
\dot{x_{1}} &= x_{2} \\ \dot{x_{2}} &= 2u-2x_{1}-x_{2} \end{align}Which on state space form is
\dot{x} &= \begin{bmatrix} 0 & 1 \\ -2 & -1 \end{bmatrix}x+\begin{bmatrix} 0 \\ 2 \end{bmatrix}u \\ y &= \begin{bmatrix} 1 & 0 \end{bmatrix}x \end{align}Where
b) We can write the controller as
Where is the feedforward part of the controller, and is the feedback of the controller. We now want to find the equilibrium point of the system
Giving us that , and where
c) Given the state error on State Space Representation form
And we have the following LQR cost function (State Feedback, and Optimal Control)
and the control input
Where , and the Positive-Definite Matrix P is the solution of the Algebraic Ricatti Equation.
GivenAlgebraic Ricatti Equation
A type of nonlinear equation that arises in the context of infinite-horizon optimal control problems in continuous or discrete time.
Continuous time algebraic Riccatti equation
Where is an unknown Positive-Definite Matrix
Link to originalPositive-Definite Matrix
A symmetric matrix with all positive eigenvalues. NOTE: All symmetric matrices have only real eigenvalues
For a matrix, , to be positive-semidefinite the following has to hold
Criterion
Given that is a symmetric real matrix
Can be written generally as
Link to original
We get (Using WolframAlpha)
\begin{bmatrix} 0 & -2 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} p_{1} & p_{2} \\ p_{2} & p_{3} \end{bmatrix} +\begin{bmatrix} p_{1} & p_{2} \\ p_{2} & p_{3} \end{bmatrix} \begin{bmatrix} 0 & 1 \\ -2 & -1 \end{bmatrix} -\begin{bmatrix} p_{1} & p_{2} \\ p_{2} & p_{3} \end{bmatrix} \begin{bmatrix} 0 \\ 2 \end{bmatrix} 4^{-1} \begin{bmatrix} 0 & 2 \end{bmatrix} \begin{bmatrix} p_{1} & p_{2} \\ p_{2} & p_{3} \end{bmatrix} +\begin{bmatrix} 5 & 0 \\ 0 & 1 \end{bmatrix} &=0\\ \dots \\ \begin{bmatrix} -4p_{2}-p_{2}²+5 & p_{1}-p_{2}-2p_{3}-p_{2}p_{3} \\ p_{1}-p_{2}-2p_{3}-p_{2}p_{3} & 2p_{2}-2p_{3}-p_{3}²+1 \end{bmatrix} &=0 \end{align}We now solve the 3 unique equations, and obtain following values for
We need to be a Positive-Definite Matrix, aka positive eigenvalues
Which obtain the following four unique solutions For
For
Where , and . Therefore we must have
Which gives us
e) The controller is previously given by:
Which we can rewrite to:
Where
f)
g) We need to prioritize the state (and therefore implicitly penalizing the rest). We can do this by increasing the first element in , so that the ratio between the first and last element is larger. This will make the controller worse at regulating the speed (), and since is down prioritized, the system will allow more energy to be spent, leading to higher values of .
Problem 2
a) & b)
Transclude of Realizations#^93dba4We have the transfer functions
We can see this as the degree of the denominator is larger than or equal to the degree of the numerator (It is proper). The degree of the transfer function is also finite (it is rational). The system is realizable
c) We find by looking at the limit
And then we can find by solving
&\hat{G}_{sp}(s) = \hat{G}(s) - D \\ &= \begin{bmatrix} \frac{s²+4s+2}{s²+2s} - 1 & \frac{3}{s+2} \\ 0 & \frac{2s²}{s²-4} - 2 \end{bmatrix} \\ &=\dots \\ & \hat{G}_{sp}(s)=\begin{bmatrix} \frac{2s+2}{s²+2s} & \frac{3}{s+2} \\ 0 & \frac{s}{s²-4} \end{bmatrix} \end{align}d) For simplicity, we rewrite the elements of as
Where
The least common demoninator is , and from the expressions we get
Meaning that and
We now find our new expressions of
e) Using the values we found for the different alphas, matrices and gives us
Where
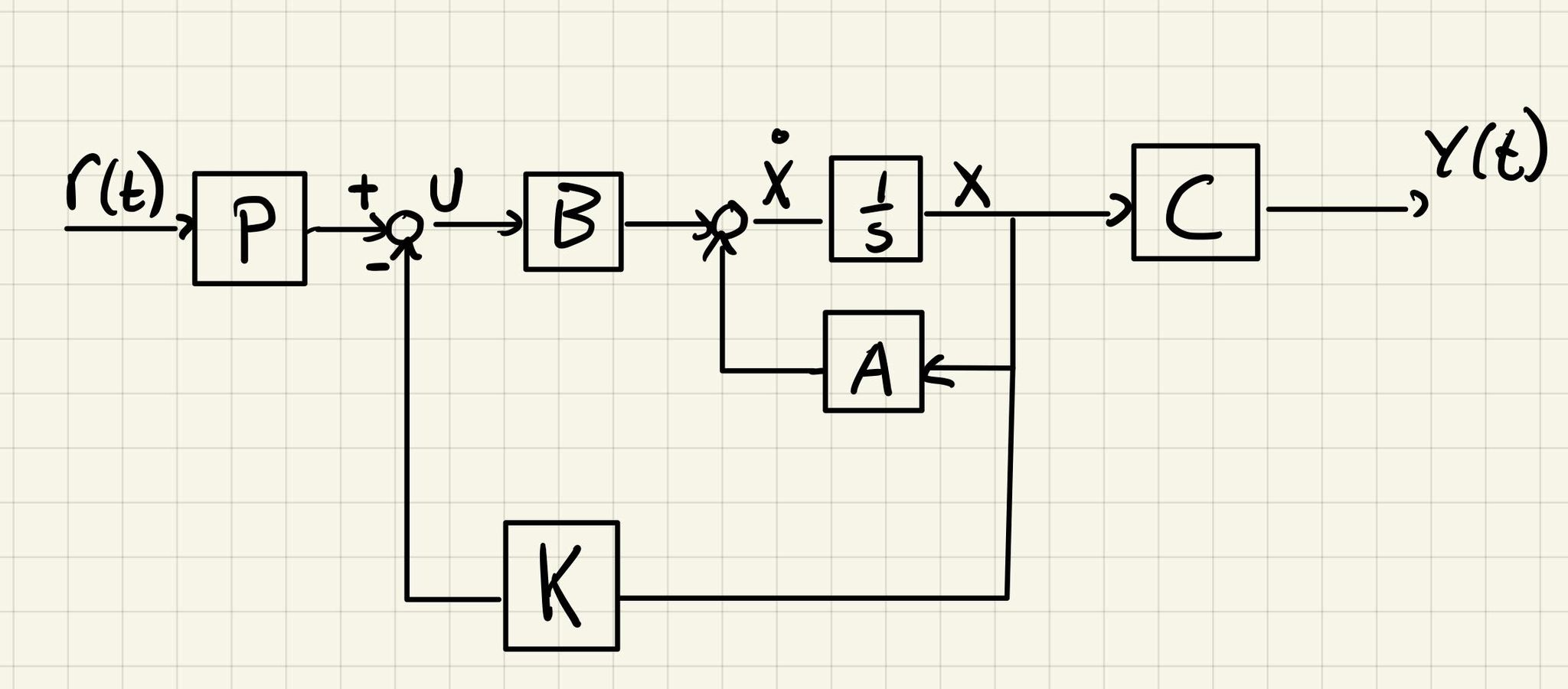
Problem 3
Given a system on State Space Representation form
Link to originalWhere
a) The observability matrix is given by
Transclude of Observability#^9093bb
Since the observability matrix has full rank (), the system is observable.
b) We have the following state estimator for the system
And since and
c) We place the poles in such a way that yields and . We set to simplify calculations
To get the correct eigenvalues, we want We therefore get the following equations
Which gives us
d)
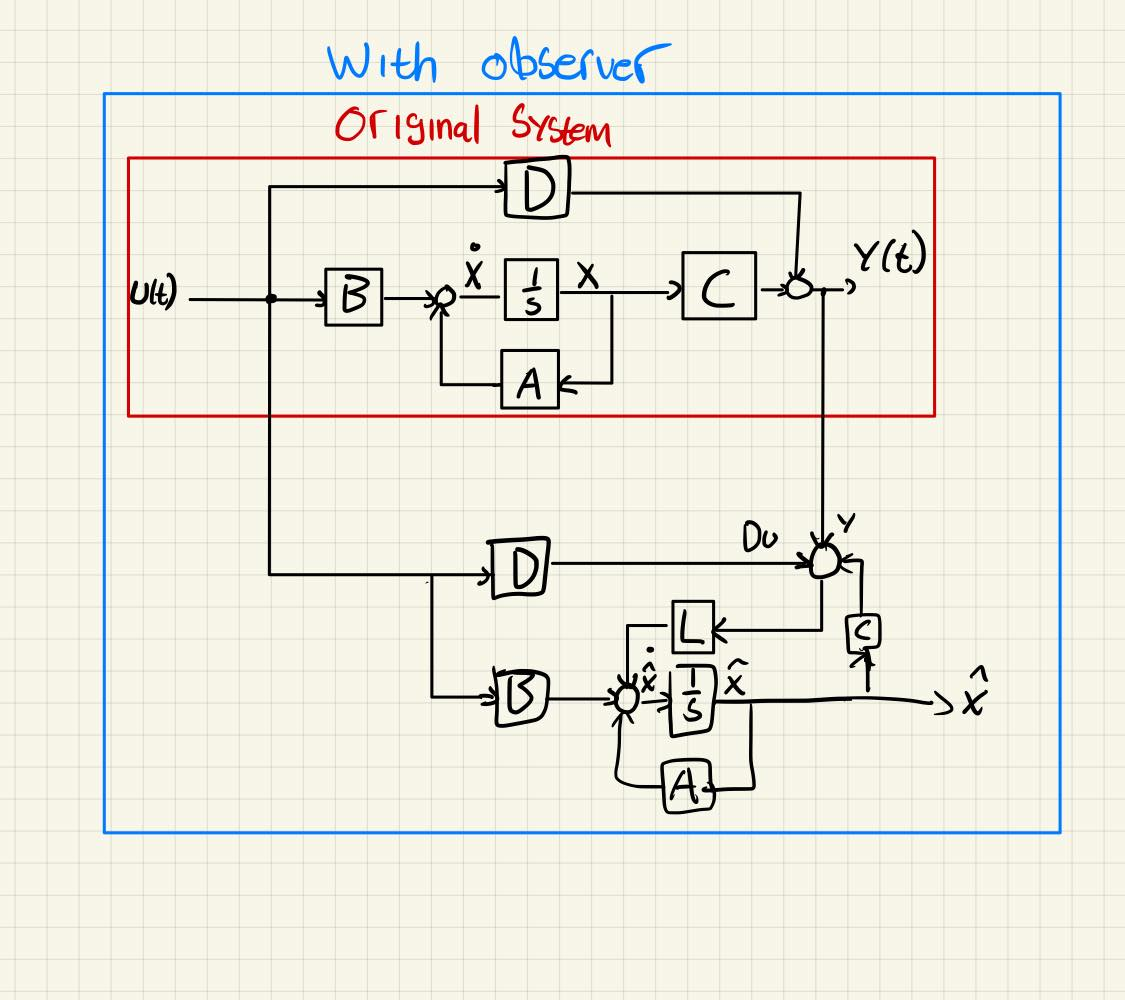
Problem 4
Given the following system
Link to originalWhere , and the state estimator
a) The second row of the matrix corresponds to the expression we got in 3b). We will now find an expression for in terms of the matrices and the states
Since → , we get
\dot{x} &= Ax-BK(e+x) \\ \dot{x} &= (A-BK)x - BKe \end{align}We can therefore write our system as
Which is what we were supposed to show where
b) We solve for the eigenvalues of
\det(H-\lambda \mathbb{I})&=\det(\begin{bmatrix} A-BK-\lambda \mathbb{I} & -BK \\ 0 & A-LC-\lambda \mathbb{I} \end{bmatrix}) =0 \\ \det(H-\lambda \mathbb{I})&=\det(A-BK-\lambda \mathbb{I})\det(A-LC-\lambda \mathbb{I})=0 \end{align}This means that the eigenvalues of are the union of the eigenvalues of and .
c) If the system is controllable, we can choose the poles of by deciding the correct . If the system is observable, we can choose the poles of by deciding the correct .
In 4b) we found out the poles of the system are the union of the eigenvalues. We can therefore choose poles freely.